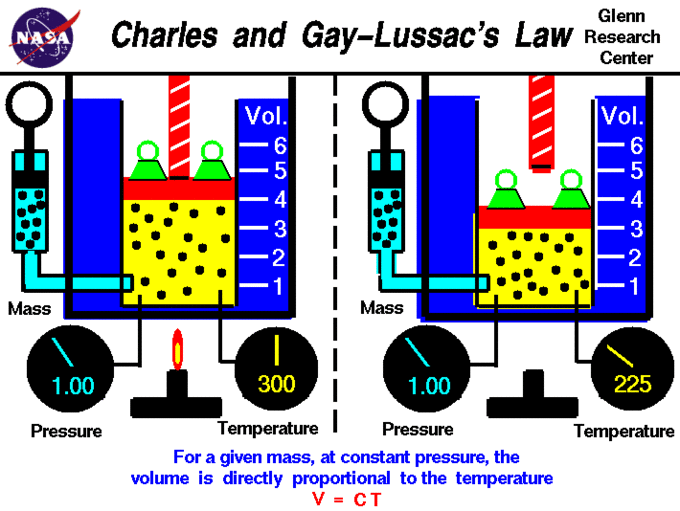
Charles' and Gay-Lussac's Law: Temperature and Volume

Charles' and Gay-Lussac's Law states that at constant pressure, temperature and volume are directly proportional.

Learning Objective

State Charles' Law and its underlying assumptions

Key Points

The lower the pressure of a gas, the greater its volume (Boyle's Law); at low pressures, $\frac{V}{273}$ will have a larger value.
Charles' and Gay-Lussac's Law can be expressed algebraically as $\frac{\Delta V}{\Delta T} = constant$ or $\frac{V_1}{T_1} = \frac{V_2}{T_2}$ .

Terms

absolute zero
the theoretical lowest possible temperature; by international agreement, absolute zero is defined as 0 K on the Kelvin scale and as −273.15° on the Celsius scale
Charles’ law
at constant pressure, the volume of a given mass of an ideal gas increases or decreases by the same factor as its temperature on the absolute temperature scale (i.e. gas expands as temperature increases)

Full Text

Charles' and Guy-Lussac's Law

Charles' Law describes the relationship between the volume and temperature of a gas. The law was ﬁrst published by Joseph Louis Gay-Lussac in 1802, but he referenced unpublished work by Jacques Charles from around 1787. This law states that at constant pressure, the volume of a given mass of an ideal gas increases or decreases by the same factor as its temperature (in Kelvin); in other words, temperature and volume are directly proportional. Stated mathematically, this relationship is:

$\frac {V_1}{T_1}=\frac{V_2}{T_2}$

Interactive: The Temperature-Volume Relationship

This model contains gas molecules on the left side and a barrier that moves when the volume of gas expands or contracts, keeping the pressure constant. Run the model and change the temperature. Why does the barrier move when the temperature changes? (Note: Although the atoms in this model are in a flat plane, volume is calculated using 0.1 nm as the depth of the container.)

Example

A car tire filled with air has a volume of 100 L at 10°C. What will the expanded volume of the tire be after driving the car has raised the temperature of the tire to 40°C?
$\frac {V_1}{T_1}=\frac{V_2}{T_2}$
$\frac {\text{100 L}}{\text{283 K}}=\frac{V_2}{\text{313 K}}$
$V_2=\text{110 L}$

V vs. T Plot and Charles' Law

A visual expression of Charles' and Gay-Lussac's Law is shown in a graph of the volume of one mole of an ideal gas as a function of its temperature at various constant pressures. The plots show that the ratio $\frac{V}{T}$ (and thus $\frac{\Delta V}{\Delta T}$) is a constant at any given pressure. Therefore, the law can be expressed algebraically as $\frac{\Delta V}{\Delta T} = \text{constant}$ or $\frac{V_1}{T_1} = \frac{V_2}{T_2}$.

Charles' and Gay–Lussac's Law

A visual expression of the law of Charles and Gay-Lussac; specifically, a chart of the volume of one mole of an ideal gas as a function of its temperature at various constant pressures.

Extrapolation to Zero Volume

If a gas contracts by 1/273 of its volume for each degree of cooling, it should contract to zero volume at a temperature of –273°C; this is the lowest possible temperature in the universe, known as absolute zero. This extrapolation of Charles' Law was the first evidence of the significance of this temperature.

Why Do the Plots for Different Pressures Have Different Slopes?

The lower a gas' pressure, the greater its volume (Boyle's Law), so at low pressures, the fraction \frac{V}{273} will have a larger value; therefore, the gas must "contract faster" to reach zero volume when its starting volume is larger.

Charles

Discusses the relationship between volume and temperature of a gas, and explains how to solve problems using Charles' Law.

[ edit ]

Prev Concept

Boyle's Law: Volume and Pressure

Avogadro's Law: Volume and Amount

Next Concept