Chemistry Textbooks Boundless Chemistry Transition Metals Bonding in Coordination Compounds: Crystal Field Theory
Chemistry Textbooks Boundless Chemistry Transition Metals
Chemistry Textbooks Boundless Chemistry
Chemistry Textbooks
Chemistry
Concept Version 11
Created by Boundless

Tetrahedral and Square Planar Complexes

Both tetrahedral and square planar complexes have a central atom with four substituents.

Learning Objective

  • Discuss the d-orbital degeneracy of square planar and tetrahedral metal complexes.

Key Points

    • In tetrahedral molecular geometry, a central atom is located at the center of four substituents, which form the corners of a tetrahedron.
    • Tetrahedral geometry is common for complexes where the metal has d0 or d10 electron configuration.
    • The CFT diagram for tetrahedral complexes has dx2−y2 and dz2 orbitals equally low in energy because they are between the ligand axis and experience little repulsion.
    • In square planar molecular geometry, a central atom is surrounded by constituent atoms, which form the corners of a square on the same plane.
    • The square planar geometry is prevalent for transition metal complexes with d8 configuration.
    • The CFT diagram for square planar complexes can be derived from octahedral complexes yet the dx2-y2 level is the most destabilized and is left unfilled.

Terms

  • degeneracy

    Having the same quantum energy level.

  • ligand

    An ion, molecule, or functional group that binds to another chemical entity to form a larger complex.

  • substituents

    Any atom, group, or radical substituted for another, or entering a molecule in place of some other part which is removed.

Full Text

Tetrahedral Complexes

In tetrahedral molecular geometry, a central atom is located at the center of four substituent atoms, which form the corners of a tetrahedron. The bond angles are approximately 109.5° when all four substituents are the same. This geometry is widespread, particularly for complexes where the metal has d0 or d10 electron configuration.

Tetrakis(triphenylphosphine)palladium

3-dimensional representation of tetrahedral Tetrakis(triphenylphosphine)palladium

For example, tetrakis(triphenylphosphine)palladium(0), a popular catalyst, and nickel carbonyl, an intermediate in nickel purification, are tetrahedral. Many complexes with incompletely filled d-subshells are tetrahedral as well—for example, the tetrahalides of iron(II), cobalt(II), and nickel(II).

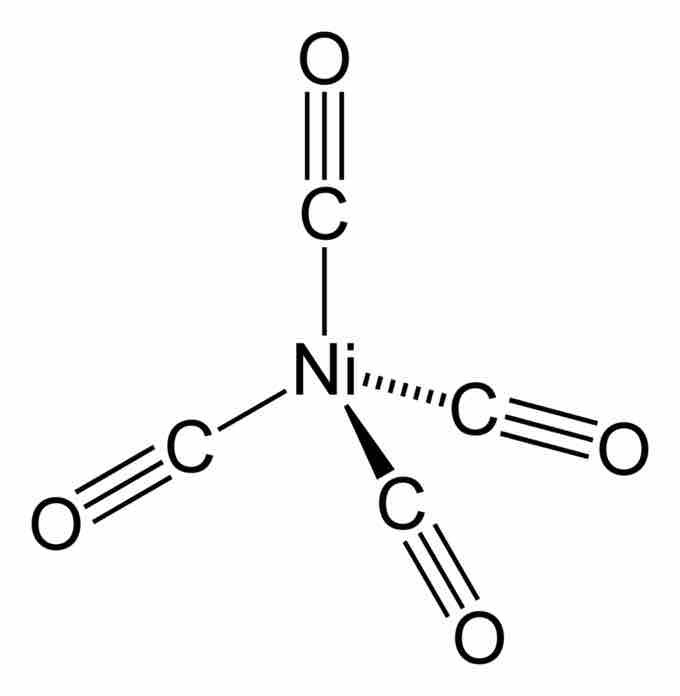
Nickel carbonyl

2-dimensional representation of tetrahedral nickel carbonyl.

Tetrahedral complexes have ligands in all of the places that an octahedral complex does not. Therefore, the crystal field splitting diagram for tetrahedral complexes is the opposite of an octahedral diagram. The dx2−dy2 and dz2 orbitals should be equally low in energy because they exist between the ligand axis, allowing them to experience little repulsion. In contrast, the dxy,dyz, and dxz axes lie directly on top of where the ligands go. This maximizes repulsion and raises energy levels.

Tetrahedral CFT splitting

Notice the energy splitting in the tetrahedral arrangement is the opposite for the splitting in octahedral arrangements.

Square Planar Complexes

In square planar molecular geometry, a central atom is surrounded by constituent atoms, which form the corners of a square on the same plane. The geometry is prevalent for transition metal complexes with d8 configuration. This includes Rh(I), Ir(I), Pd(II), Pt(II), and Au(III). Notable examples include the anticancer drugs cisplatin [PtCl2(NH3)2] and carboplatin.

Carboplatin

2- and 3-dimensional representations of the anti-cancer drug carboplatin

In principle, square planar geometry can be achieved by flattening a tetrahedron. As such, the interconversion of tetrahedral and square planar geometries provides a pathway for the isomerization of tetrahedral compounds. For example, tetrahedral nickel(II) complexes such as NiBr2(PPh3)2 undergo this change reversibly.

The removal of a pair of ligands from the z-axis of an octahedron leaves four ligands in the x-y plane. Therefore, the crystal field splitting diagram for square planar geometry can be derived from the octahedral diagram. The removal of the two ligands stabilizes the dz2 level, leaving the dx2-y2 level as the most destabilized. Consequently, the dx2-y2 remains unoccupied in complexes of metals with the d8 configuration. These compounds typically have sixteen valence electrons (eight from ligands, eight from the metal).

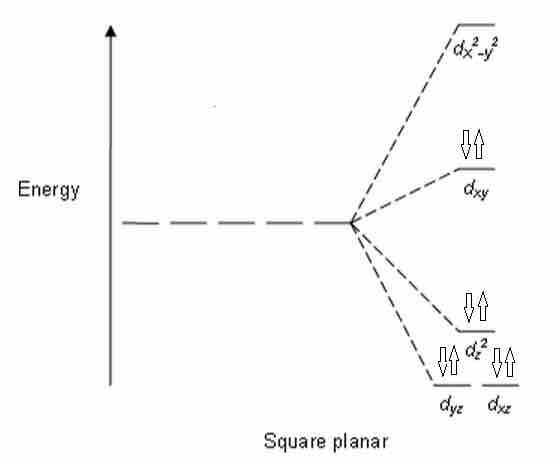
CFT energy diagram for square planar complexes

Notice how the dx2 - y2 orbital is unfilled.

[ edit ]
Edit this content
Prev Concept
Octahedral Complexes
Color
Next Concept