In , nrepresents the number of periods. A period is just a general term for a length of time. It can be anything- one month, one year, one decade- but it must be clearly defined and fixed. The length of one period must be the same at the beginning of an investment and at the end. It is also part of the units of the discount rate: if one period is one year, the discount rate must be defined as X% per year. If one period is one month, the discount rate must be X% per month.
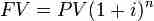
FV of a single payment
The PV and FV are directly related.
The number of periods corresponds to the number of times the interest is accrued. In the case of simple interest the number of periods, t, is multiplied by their interest rate. This makes sense because if you earn $30 of interest in the first period, you also earn $30 of interest in the last period, so the total amount of interest earned is simple t x $30.
Simple interest is rarely used in comparison to compound interest . In compound interest, the interest in one period is also paid on all interest accrued in previous periods. Therefore, there is an exponential relationship between PV and FV, which is reflected in (1+i)n .

Car
Car loans, mortgages, and student loans all generally have compound interest.
For both forms of interest, the number of periods varies jointly with FV and inversely with PV. Logically, if more time passes between the present and the future, the FV must be higher or the PV lower (assuming the discount rate remains constant).