Like any other form of electrical circuitry device, capacitors can be used in combination in circuits. These combinations can be in series (in which multiple capacitors can be found along the same path of wire) and in parallel (in which multiple capacitors can be found along different paths of wire).
Capacitors in Series
Like in the case of resistors in parallel, the reciprocal of the circuit's total capacitance is equal to the sum of the reciprocals of the capacitance of each individual capacitor :
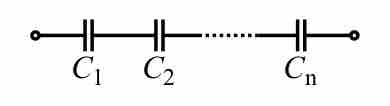
Capacitors in Series
This image depicts capacitors C1, C2 and so on until Cn in a series.
This can also be expressed as:
Parallel Capacitors
Total capacitance for a circuit involving several capacitors in parallel (and none in series) can be found by simply summing the individual capacitances of each individual capacitor .
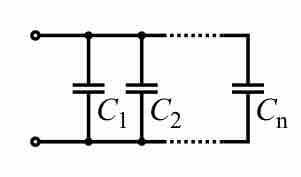
Parallel Capacitors
This image depicts capacitors C1, C2, and so on until Cn in parallel.
Capacitors in Series and in Parallel
It is possible for a circuit to contain capacitors that are both in series and in parallel. To find total capacitance of the circuit, simply break it into segments and solve piecewise .
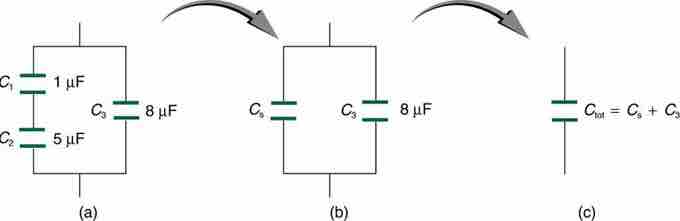
Capacitors in Series and in Parallel
The initial problem can be simplified by finding the capacitance of the series, then using it as part of the parallel calculation.
The circuit shown in (a) contains C1 and C2 in series. However, these are both in parallel with C3. If we find the capacitance for the series including C1 and C2, we can treat that total as that from a single capacitor (b). This value can be calculated as approximately equal to 0.83 μF.
With effectively two capacitors left in parallel, we can add their respective capacitances (c) to find the total capacitance for the circuit. This sum is approximately 8.83 μF.