Conduction
Conduction is the transfer of heat through stationary matter by physical contact. (The matter is stationary on a macroscopic scale—we know there is thermal motion of the atoms and molecules at any temperature above absolute zero. ) Heat transferred from an electric stove to the bottom of a pot is an example of conduction.
Some materials conduct thermal energy faster than others. For example, the pillow in your room may the same temperature as the metal doorknob, but the doorknob feels cooler to the touch. In general, good conductors of electricity (metals like copper, aluminum, gold, and silver) are also good heat conductors, whereas insulators of electricity (wood, plastic, and rubber) are poor heat conductors.
Microscopic Description of Conduction
On a microscopic scale, conduction occurs as rapidly moving or vibrating atoms and molecules interact with neighboring particles, transferring some of their kinetic energy. Heat is transferred by conduction when adjacent atoms vibrate against one another, or as electrons move from one atom to another. Conduction is the most significant means of heat transfer within a solid or between solid objects in thermal contact. Conduction is greater in solids because the network of relatively close fixed spatial relationships between atoms helps to transfer energy between them by vibration.
Fluids and gases are less conductive than solids. This is due to the large distance between atoms in a fluid or (especially) a gas: fewer collisions between atoms means less conduction .
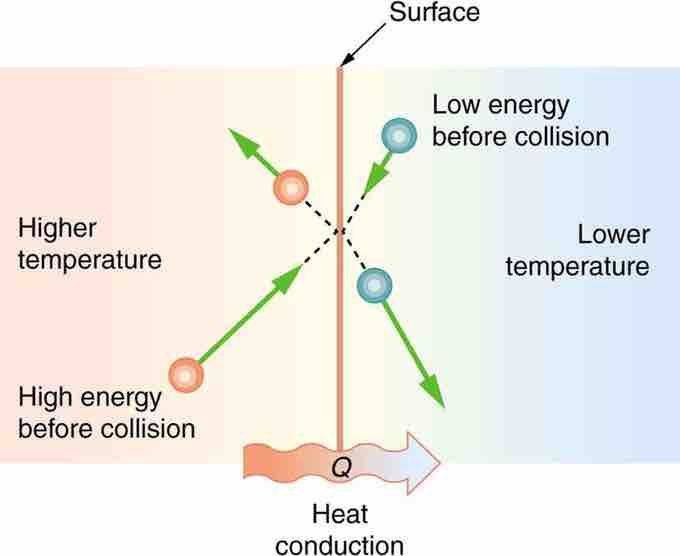
Microscopic Illustration of Conduction
he molecules in two bodies at different temperatures have different average kinetic energies. Collisions occurring at the contact surface tend to transfer energy from high-temperature regions to low-temperature regions. In this illustration, a molecule in the lower temperature region (right side) has low energy before collision, but its energy increases after colliding with the contact surface. In contrast, a molecule in the higher temperature region (left side) has high energy before collision, but its energy decreases after colliding with the contact surface.
The (average) kinetic energy of a molecule in the hot body is higher than in the colder body. If two molecules collide, an energy transfer from the hot to the cold molecule occurs (see the above figure). The cumulative effect from all collisions results in a net flux of heat from the hot body to the colder body. The heat flux thus depends on the temperature difference T=Thot−Tcold. Therefore, you will get a more severe burn from boiling water than from hot tap water. Conversely, if the temperatures are the same, the net heat transfer rate falls to zero, and equilibrium is achieved. Owing to the fact that the number of collisions increases with increasing area, heat conduction depends on the cross-sectional area. If you touch a cold wall with your palm, your hand cools faster than if you just touch it with your fingertip.
Factors Affecting the Rate of Heat Transfer Through Conduction
In addition to temperature and cross-sectional area, another factor affecting conduction is the thickness of the material through which the heat transfers. Heat transfer from the left side to the right side is accomplished by a series of molecular collisions. The thicker the material, the more time it takes to transfer the same amount of heat. If you get cold during the night, you may retrieve a thicker blanket to keep warm .
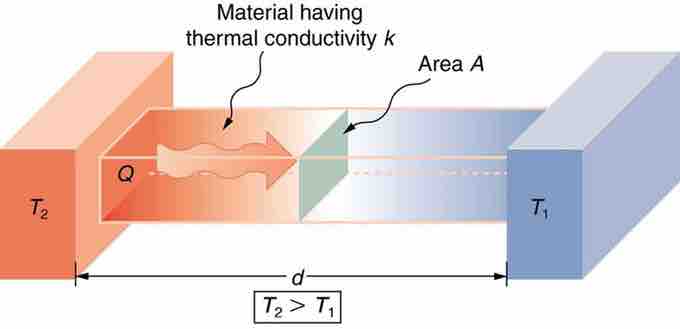
Effect of Thickness on Heat Conduction
Heat conduction occurs through any material, represented here by a rectangular bar. The temperature of the material is T2 on the left and T1 on the right, where T2 is greater than T1. The rate of heat transfer by conduction is directly proportional to the surface area A, the temperature difference T2−T1, and the substance's conductivity k. The rate of heat transfer is inversely proportional to the thickness d.
Lastly, the heat transfer rate depends on the material properties described by the coefficient of thermal conductivity. All four factors are included in a simple equation that was deduced from and is confirmed by experiments. The rate of conductive heat transfer through a slab of material, such as the one in the figure above is given by
where Q/t is the rate of heat transfer in Joules per second (Watts), k is the thermal conductivity of the material, A and d are its surface area and thickness, and (T2−T1) is the temperature difference across the slab.