Diffraction
As we explained in a previous atom, diffraction is defined as the bending of a wave around the edges of an opening or obstacle. Diffraction is a phenomenon all wave types can experience. It is explained by the Huygens-Fresnel Principle, and the principal of superposition of waves. The former states that every point on a wavefront is a source of wavelets. These wavelets spread out in the forward direction, at the same speed as the source wave. The new wavefront is a line tangent to all of the wavelets. The superposition principle states that at any point, the net result of multiple stimuli is the sum of all stimuli.
Single Slit Diffraction
In single slit diffraction, the diffraction pattern is determined by the wavelength and by the length of the slit. Figure 1 shows a visualization of this pattern. This is the most simplistic way of using the Huygens-Fresnel Principle, which was covered in a previous atom, and applying it to slit diffraction. But what happens when the slit is NOT the exact (or close to exact) length of a single wave?
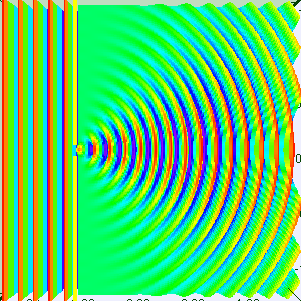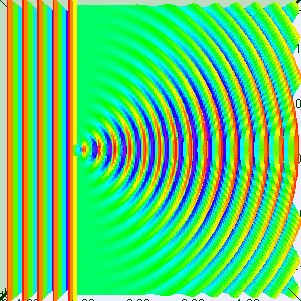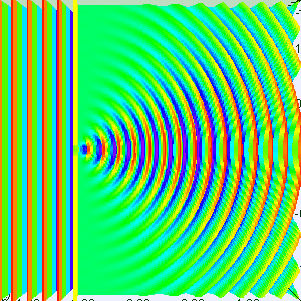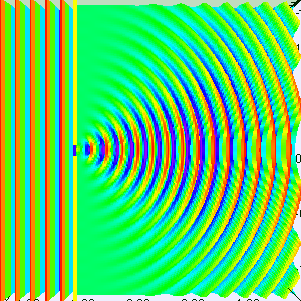
Single Slit Diffraction - One Wavelength
Visualization of single slit diffraction when the slit is equal to one wavelength.
A slit that is wider than a single wave will produce interference-like effects downstream from the slit. It is easier to understand by thinking of the slit not as a long slit, but as a number of point sources spaced evenly across the width of the slit. This can be seen in Figure 2 .

Single Slit Diffraction - Four Wavelengths
This figure shows single slit diffraction, but the slit is the length of 4 wavelengths.
To examine this effect better, lets consider a single monochromatic wavelength. This will produce a wavefront that is all in the same phase. Downstream from the slit, the light at any given point is made up of contributions from each of these point sources. The resulting phase differences are caused by the different in path lengths that the contributing portions of the rays traveled from the slit.
The variation in wave intensity can be mathematically modeled. From the center of the slit, the diffracting waves propagate radially. The angle of the minimum intensity (θmin) can be related to wavelength (λ) and the slit's width (d) such that:
The intensity (I) of waves at any angle can also be calculated as a relation to slit width, wavelength and intensity of the original waves before passing through the slit:
where x is equal to: