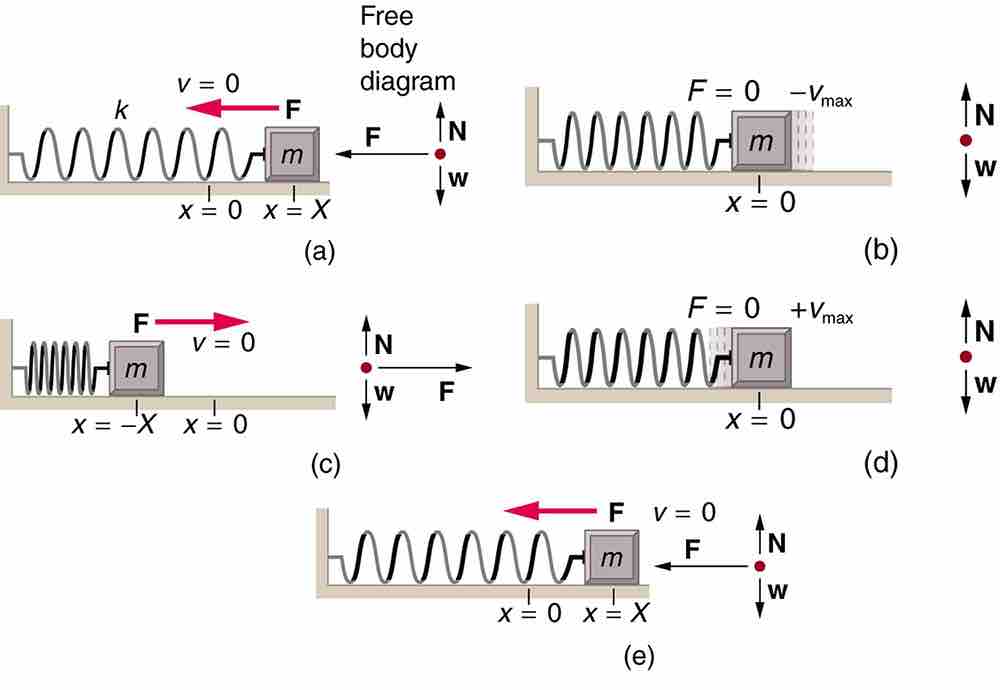
Motion of a mass on an ideal spring
An object attached to a spring sliding on a frictionless surface is an uncomplicated simple harmonic oscillator. When displaced from equilibrium, the object performs simple harmonic motion that has an amplitude X and a period T. The object's maximum speed occurs as it passes through equilibrium. The stiffer the spring is, the smaller the period T. The greater the mass of the object is, the greater the period T. (a) The mass has achieved its greatest displacement X to the right and now the restoring force to the left is at its maximum magnitude. (b) The restoring force has moved the mass back to its equilibrium point and is now equal to zero, but the leftward velocity is at its maximum. (c) The mass's momentum has carried it to its maximum displacement to the right. The restoring force is now to the right, equal in magnitude and opposite in direction compared to (a). (d) The equilibrium point is reach again, this time with momentum to the right. (e) The cycle repeats.
Source
Boundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources: