When studying waves, it is helpful to use a string to observe the physical properties of waves visually. Imagine you are holding one end of a string, and the other end is secured and the string is pulled tight. Now, if you were to flick the string either up and down. The wave that occurs due to this motion is called a transverse wave. A transverse wave is defined as a wave where the movement of the particles of the medium is perpendicular to the direction of the propagation of the wave. Figure 1 shows this in a diagram. In this case, the medium through which the waves propagate is the rope. The wave traveled from one end to the other, while the rope moved up and down.
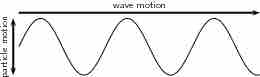
Figure 1
In transverse waves, the media the wave is traveling in moves perpendicular to the direction of the wave.
Wave Properties
Transverse waves have what are called peaks and troughs. The peak is the crest, or top point of the wave and the trough is the valley or bottom point of the wave. Refer to Figure 2 for a visual representation of these terms.The amplitude is the maximum displacement of a particle from its equilibrium position.Wavelength, usually denoted with a lambda (λ) and measured in meters, is the distance from either one peak to the next peak, or one trough to the next trough.Period, usually denoted as T and measured in seconds, is the time it takes for two successive peaks, or one wavelength, to pass through a fixed point.Frequency, f, is the number of wavelengths that pass through a given point in 1 second. Frequency is measured by taking the reciprocal of a period:

Figure 2
Peaks are the top most points of the waves and troughs are the bottom, or valleys of the waves.
Speed of a Wave on a String
Velocity is found by dividing the distance traveled by the time it took to travel that distance. In waves, this is found by dividing the wavelength by the period:
Speed of a Wave on a Vibrating String
Another example of waves on strings are of the waves on vibrating strings, such as in musical instruments. Pianos and guitars both use vibrating strings to produce music. In these cases, the frequency is what characterizes the pitch and therefore the note. The speed of a wave on this kind of string is proportional to the square root of the tension in the string and inversely proportional to the square root of the linear density of the string: