What is the difference between hypothesis testing and confidence intervals? When we conduct a hypothesis test, we assume we know the true parameters of interest. When we use confidence intervals, we are estimating the parameters of interest.
Explanation of the Difference
Confidence intervals are closely related to statistical significance testing. For example, if for some estimated parameter
More generally, given the availability of a hypothesis testing procedure that can test the null hypothesis
In consequence, if the estimates of two parameters (for example, the mean values of a variable in two independent groups of objects) have confidence intervals at a given
While the formulations of the notions of confidence intervals and of statistical hypothesis testing are distinct, in some senses and they are related, and are complementary to some extent. While not all confidence intervals are constructed in this way, one general purpose approach is to define a
It may be convenient to say that parameter values within a confidence interval are equivalent to those values that would not be rejected by a hypothesis test, but this would be dangerous. In many instances the confidence intervals that are quoted are only approximately valid, perhaps derived from "plus or minus twice the standard error," and the implications of this for the supposedly corresponding hypothesis tests are usually unknown.
It is worth noting that the confidence interval for a parameter is not the same as the acceptance region of a test for this parameter, as is sometimes assumed. The confidence interval is part of the parameter space, whereas the acceptance region is part of the sample space. For the same reason, the confidence level is not the same as the complementary probability of the level of significance.
Confidence Interval
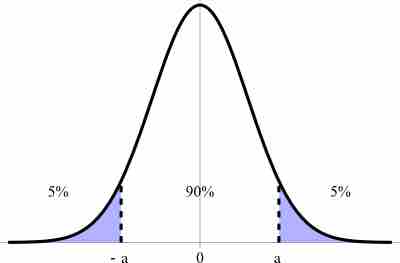
This graph illustrates a 90% confidence interval on a standard normal curve.