Finding the Area Under the Normal Curve

To calculate the probability that a variable is within a range in the normal distribution, we have to find the area under the normal curve. In order to do this, we use a $z$-score table. (Same as in the process of standardization discussed in the previous section).

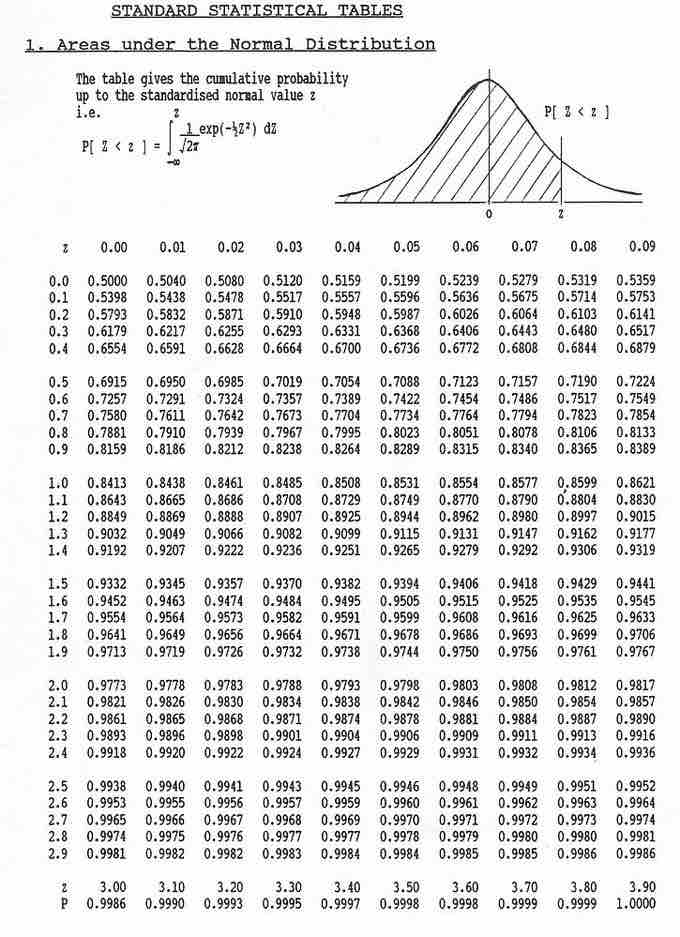
Areas Under the Normal Curve

This table gives the cumulative probability up to the standardized normal value $z$.

These tables can seem a bit daunting; however, the key is knowing how to read them.

• The left most column tells you how many standard deviations above the the mean to 1 decimal place.
• The top row gives the second decimal place.
• The intersection of a row and column gives the probability.

For example, if we want to know the probability that a variable is no more than 0.51 standard deviations above the mean, we find select the 6^th row down (corresponding to 0.5) and the 2^nd column (corresponding to 0.01). The intersection of the 6^th row and 2^nd column is 0.6950. This tells us that there is a 69.50% percent chance that a variable is less than 0.51 sigmas above the mean.

Notice that for 0.00 standard deviations, the probability is 0.5000. This shows us that there is equal probability of being above or below the mean.

Consider the following as a simple example: find $P(Z\leq 1.5)$.

This problem essentially asks what is the probability that a variable is less than 1.5 standard deviations above the mean. On the table of values, find the row that corresponds to 1.5 and the column that corresponds to 0.00. This gives us a probability of 0.933.

The following is another simple example: find $P(Z\geq 1.17)$.

This problem essentially asks what is the probability that a variable is MORE than 1.17 standard deviation above the mean. On the table of values, find the row that corresponds to 1.1 and the column that corresponds to 0.07. This gives us a probability of 0.8790. However, this is the probability that the value is less than 1.17 sigmas above the mean. Since all the probabilities must sum to 1:

$P(Z>1.17) = 1-P(Z<1.17) = 0.121$

As a final example: find $P(-1.16\leq Z\leq 1.32)$.

This example is a bit tougher. The problem can be rewritten in the form below.

$P(-1.16\leq Z\leq 1.32) = P(Z\leq 1.32) - P(Z\leq -1.16)$

The difficulty arrises from the fact that our table of values does not allow us to directly calculate $P(Z\leq -1.16)$. However, we can use the symmetry of the distribution, as follows:

$P(Z\leq -1.16) = 1-P(Z\leq 1.16) = 0.1230$

So, we can say that:

$P(-1.16\leq Z \leq 1.32) = 0.9066 - 0.1230 = 0.7836$