Directional Hypotheses and One-Tailed Tests

When putting together a hypothesis test, consideration of directionality is critical. The vast majority of hypothesis tests involve either a point hypothesis, two-tailed hypothesis or one-tailed hypothesis. A one-tailed test or two-tailed test are alternative ways of computing the statistical significance of a data set in terms of a test statistic, depending on whether only one direction is considered extreme (and unlikely) or both directions are considered extreme. The terminology "tail" is used because the extremes of distributions are often small, as in the normal distribution or "bell curve" . If the test statistic is always positive (or zero), only the one-tailed test is generally applicable, while if the test statistic can assume positive and negative values, both the one-tailed and two-tailed test are of use.

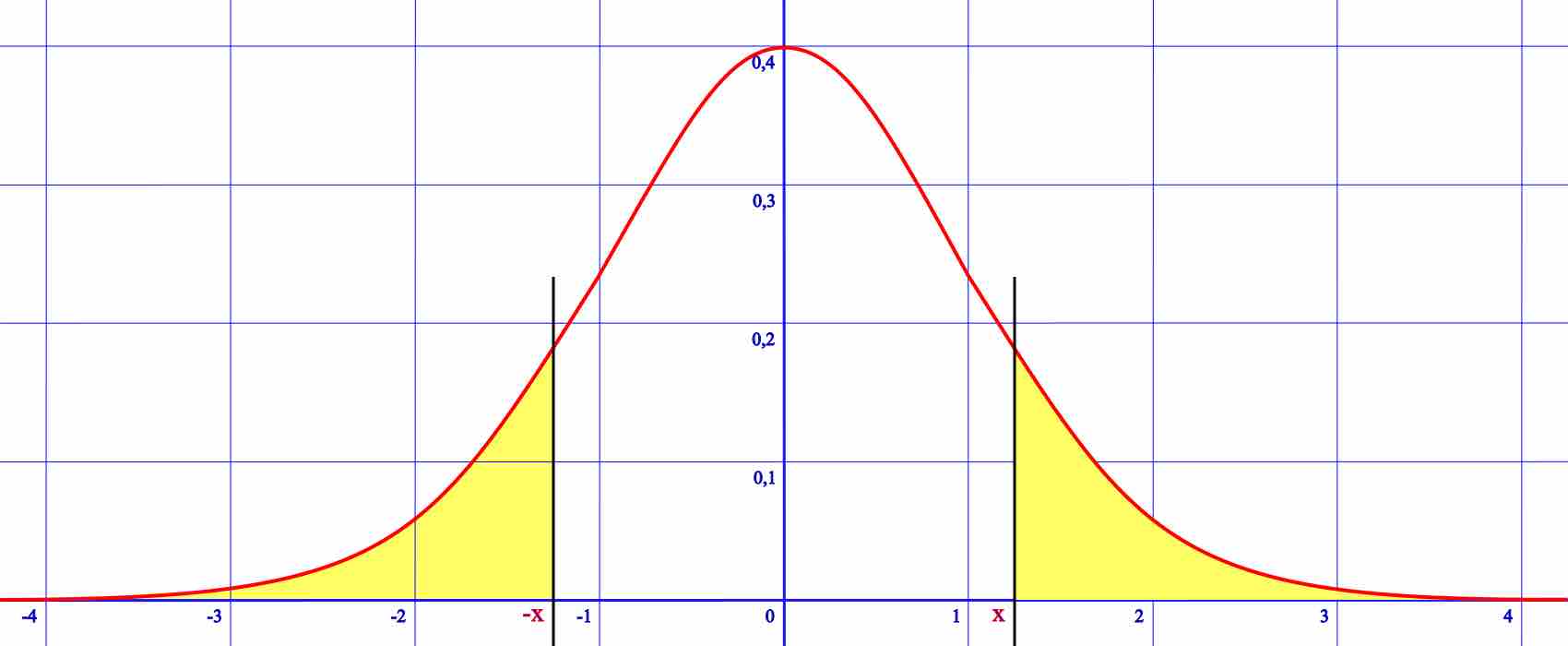
Two-Tailed Test

A two-tailed test corresponds to both extreme negative and extreme positive directions of the test statistic, here the normal distribution.

A one-tailed hypothesis is a hypothesis in which the value of a parameter is specified as being either:

• above or equal to a certain value, or
• below or equal to a certain value.

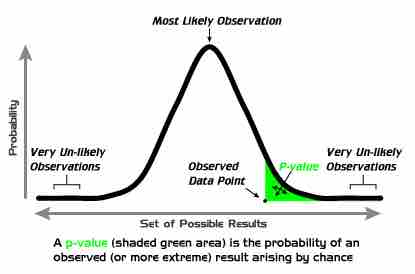
One-Tailed Test

A one-tailed test, showing the $p$-value as the size of one tail.

An example of a one-tailed null hypothesis, in the medical context, would be that an existing treatment, $A$, is no worse than a new treatment, $B$. The corresponding alternative hypothesis would be that $B$ is better than $A$. Here, if the null hypothesis is not rejected (i.e., there is no reason to reject the hypothesis that $A$ is at least as good as $B$) the conclusion would be that treatment $A$ should continue to be used. If the null hypothesis were rejected (i.e., there is evidence that $B$ is better than $A$) the result would be that treatment $B$ would be used in future. An appropriate hypothesis test would look for evidence that $B$ is better than $A$ not for evidence that the outcomes of treatments $A$ and $B$ are different. Formulating the hypothesis as a "better than" comparison is said to give the hypothesis directionality.

Applications of One-Tailed Tests

One-tailed tests are used for asymmetric distributions that have a single tail (such as the chi-squared distribution, which is common in measuring goodness-of-fit) or for one side of a distribution that has two tails (such as the normal distribution, which is common in estimating location). This corresponds to specifying a direction. Two-tailed tests are only applicable when there are two tails, such as in the normal distribution, and correspond to considering either direction significant.

In the approach of Ronald Fisher, the null hypothesis $H_0$ will be rejected when the $p$-value of the test statistic is sufficiently extreme (in its sampling distribution) and thus judged unlikely to be the result of chance. In a one-tailed test, "extreme" is decided beforehand as either meaning "sufficiently small" or "sufficiently large" – values in the other direction are considered insignificant. In a two-tailed test, "extreme" means "either sufficiently small or sufficiently large", and values in either direction are considered significant. For a given test statistic there is a single two-tailed test and two one-tailed tests (one each for either direction). Given data of a given significance level in a two-tailed test for a test statistic, in the corresponding one-tailed tests for the same test statistic it will be considered either twice as significant (half the $p$-value) if the data is in the direction specified by the test or not significant at all ($p$-value above 0.5) if the data is in the direction opposite that specified by the test.

For example, if flipping a coin, testing whether it is biased towards heads is a one-tailed test. Getting data of "all heads" would be seen as highly significant, while getting data of "all tails" would not be significant at all ($p=1$). By contrast, testing whether it is biased in either direction is a two-tailed test, and either "all heads" or "all tails" would both be seen as highly significant data.