Sampling is concerned with the selection of a subset of individuals from within a statistical population to estimate characteristics of the whole population . Two advantages of sampling are that the cost is lower and data collection is faster than measuring the entire population.
Random Sampling
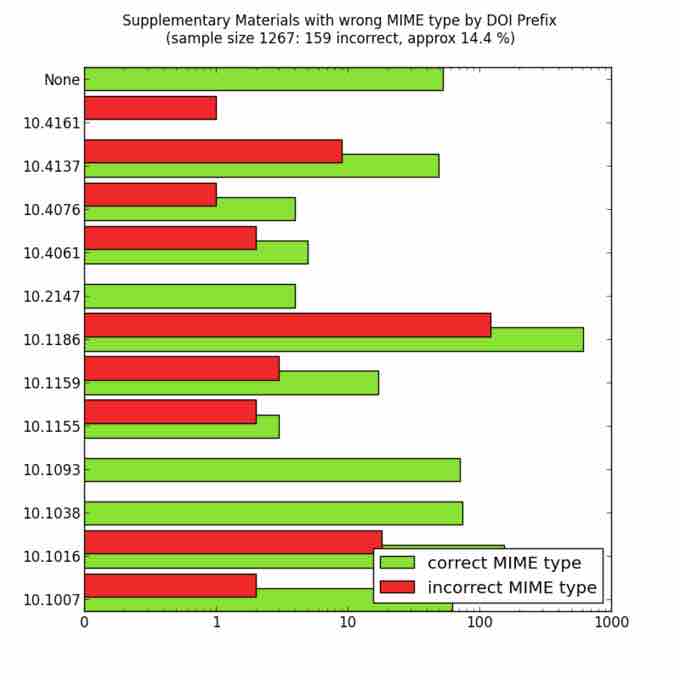
MIME types of a random sample of supplementary materials from the Open Access subset in PubMed Central as of October 23, 2012. The colour code means that the MIME type of the supplementary files is indicated correctly (green) or incorrectly (red) in the XML at PubMed Central.
Each observation measures one or more properties (such as weight, location, color) of observable bodies distinguished as independent objects or individuals. In survey sampling, weights can be applied to the data to adjust for the sample design, particularly stratified sampling (blocking). Results from probability theory and statistical theory are employed to guide practice. In business and medical research, sampling is widely used for gathering information about a population.
A simple random sample is a subset of individuals chosen from a larger set (a population). Each individual is chosen randomly and entirely by chance, such that each individual has the same probability of being chosen at any stage during the sampling process and each subset of
Simple random sampling is a basic type of sampling, since it can be a component of other more complex sampling methods. The principle of simple random sampling is that every object has the same possibility to be chosen. For example,
In small populations and often in large ones, such sampling is typically done "without replacement" (i.e., one deliberately avoids choosing any member of the population more than once). Although simple random sampling can be conducted with replacement instead, this is less common and would normally be described more fully as simple random sampling with replacement. Sampling done without replacement is no longer independent, but still satisfies exchangeability. Hence, many results still hold. Further, for a small sample from a large population, sampling without replacement is approximately the same as sampling with replacement, since the odds of choosing the same individual twice is low.
An unbiased random selection of individuals is important so that, in the long run, the sample represents the population. However, this does not guarantee that a particular sample is a perfect representation of the population. Simple random sampling merely allows one to draw externally valid conclusions about the entire population based on the sample.
Conceptually, simple random sampling is the simplest of the probability sampling techniques. It requires a complete sampling frame, which may not be available or feasible to construct for large populations. Even if a complete frame is available, more efficient approaches may be possible if other useful information is available about the units in the population.
Advantages are that it is free of classification error, and it requires minimum advance knowledge of the population other than the frame. Its simplicity also makes it relatively easy to interpret data collected via SRS. For these reasons, simple random sampling best suits situations where not much information is available about the population and data collection can be efficiently conducted on randomly distributed items, or where the cost of sampling is small enough to make efficiency less important than simplicity. If these conditions are not true, stratified sampling or cluster sampling may be a better choice.