Circles are all around you in everyday life, from tires on cars to buttons on coats, as well as on the tops of bowls, glasses, and water bottles. Ellipses are less common. One example is the orbits of planets, but you should be able to find the area of a circle or an ellipse, or the circumference of a circle, based on information given to you in a problem. Circles and ellipses are examples of conic sections, which are curves formed by the intersection of a plane with a cone.
Some sample problems are shown below, with solutions worked out.
Exercise 1
Let's say you are a gardener, and you have just planted a lot of flowers that you want to water. The flower bed is 15 feet wide, and 15 feet long. You are using a circular sprinkler system, and the water reaches 6 feet out from the center. The sprinkler is located, from the bottom left corner of the bed, 7 feet up, and 6 feet over.
- If the flower bed was a graph with the bottom left corner being the origin, what would the equation of the circle be?
- What is the area being watered by the sprinkler?
- What percentage of the garden that is being watered?
Answer
If the bottom left corner is the origin, it has coordinates
The area that is watered by the sprinkler can be labeled
The first step to finding the percentage of the garden that is being watered is to check that none of the water is falling outside the garden. The sprinkler is at coordinate
Once we know that the area that is watered is completely inside the garden, the percentage of the garden that is watered can be found by dividing the area watered by the total area of the garden, and then multiplying by
Exercise 2
Now, let's take it the other way.
- What are the coordinates of the center of the circle?
- What is the radius?
- Draw the circle.
- Find two points on the circle and plug them into the equation to make sure your drawing is correct.
Answer
The center of the circle can be found by comparing the equation in this exercise to the equation of a circle:
The center of the circle is at coordinate
The radius of the circle is
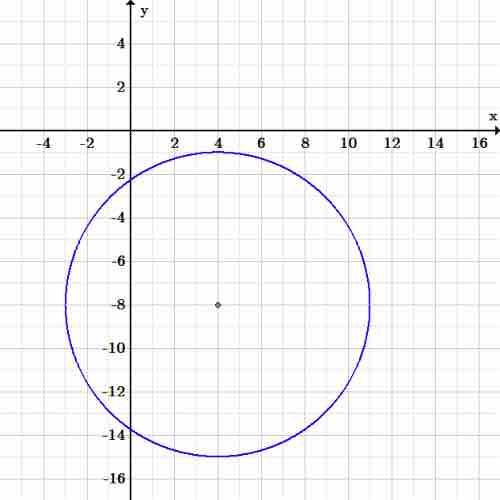
Exercise 2 circle
Graph of the circle
There are many points you could choose. For example, the point
The left side is equal to the right side of the equation, and so this is a valid point on the circle.
The leftmost point on the circle is
The left side is equal to the right side of the equation, and so this is a valid point on the circle.
Exercise 3
- Put
$2x^2+2y^2+8x+24y+60=0$ into the standard circle form:$(x-h)^2+(y-k)^2=r^2$ . - What is the center and the radius of the circle?
- Draw the circle.
- Find two points on the circle and plug them into the equation to make sure your drawing is correct.
Answer
First, divide the equation by the coefficient of
Next, collect
Now, complete the square in both parentheses, subtracting or adding the necessary constant to both sides of the equation:
Notice that each term is a perfect square, which gives:
This is now in the standard form for the equation of a circle.
The center of the circle is at coordinate
The radius of the circle is
It is fine to leave the value of
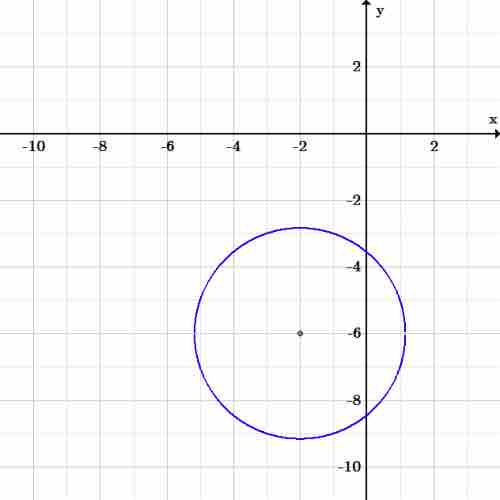
Exercise 3 circle
Graph of the circle
There are many points you could choose. For example,
Both are valid points on the circle.
Exercise 4
- Put the equation
$\displaystyle{ \frac{4x^2}{9} + 25y^2 = 1 }$ into standard form. - What is the center?
- How long is the major axis?
- How long is the minor axis?
- Graph it.
Answer
This almost looks like an ellipse in standard form, doesn't it? It even has a number on the right side. But it isn't. There is no room in the standard form for the values
Rewrite the left-hand term,
Rewrite the right-hand term,
The equation is now:
From the standard equation,
The major axis depends which is longer,
Since
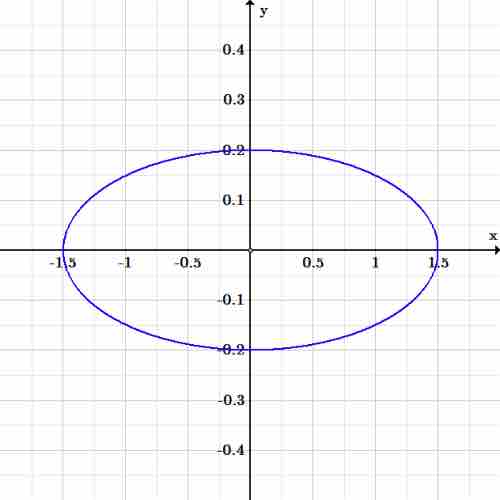
Exercise 4 ellipse
Graph of the ellipse