Applications of Taylor Series

Uses of the Taylor series for analytic functions include:

1. The partial sums (the Taylor polynomials) of the series can be used as approximations of the entire function. These approximations are often good enough if sufficiently many terms are included. Approximations using the first few terms of a Taylor series can make otherwise unsolvable problems possible for a restricted domain; this approach is often used in physics.

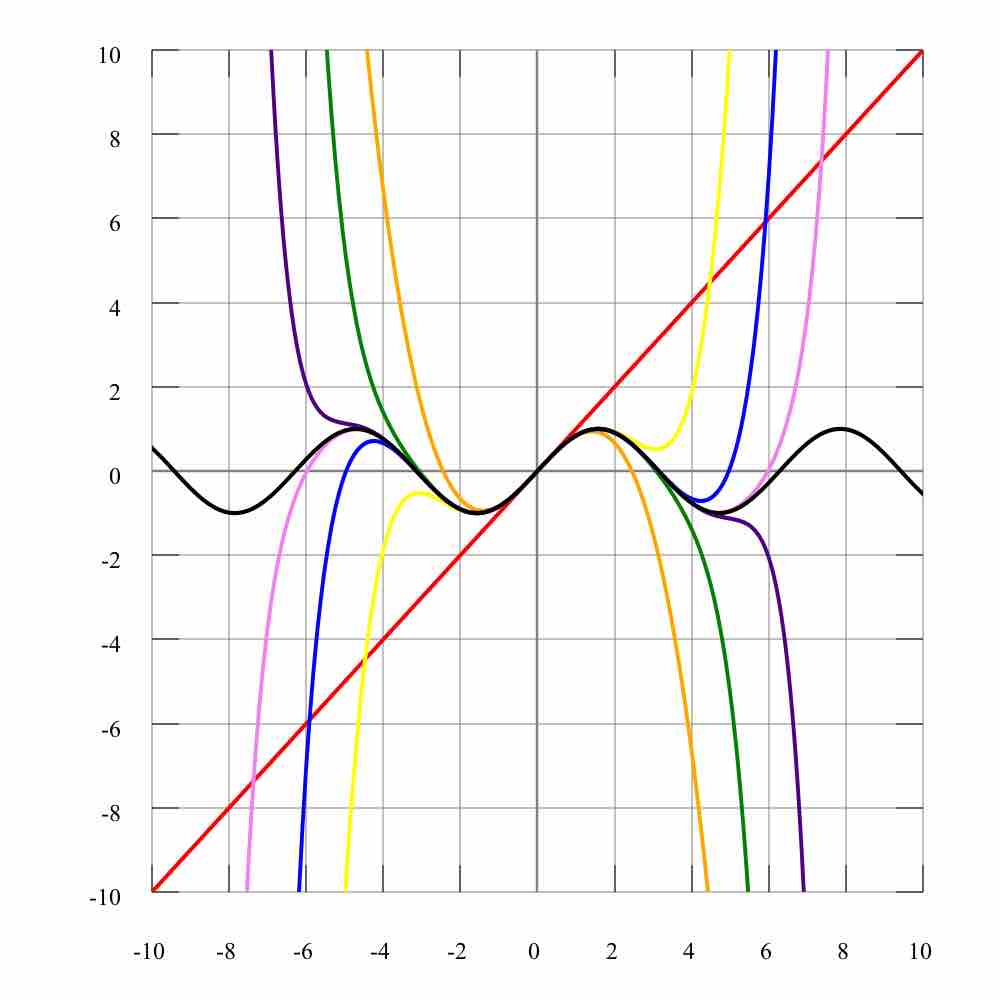
Taylor Polynomials

As more terms are added to the Taylor polynomial, it approaches the correct function. This image shows $\sin x$ and its Taylor approximations, polynomials of degree 1, 3, 5, 7, 9, 11 and 13.

2. Differentiation and integration of power series can be performed term by term and is hence particularly easy. Taylor series is especially useful in evaluating definite integrals. For example, to evaluate $\int_{0}^{1} e^{x^3} \, dx$, the Taylor series expansion of $e^t= \sum_{n=0}^{\infty} \frac{1}{n! } \, t^n$and the substitution of $t=x^3$ can be used. Since each term in the summation can be integrated separately, we can evaluate the definite integral as long as the sum converges.

3. An analytic function is uniquely extended to a holomorphic function on an open disk in the complex plane. This makes the machinery of complex analysis available.

4. The (truncated) series can be used to compute function values numerically. This is particularly useful in evaluating special mathematical functions (such as Bessel function).

5. Algebraic operations can be done readily on the power series representation; for instance the Euler's formula follows from Taylor series expansions for trigonometric and exponential functions. $e^{ix}$ can be found from the Taylor expansion of $\cos(x)$ and $\sin(x)$:

$\displaystyle{\cos(x) = 1-\frac{x^2}{2!}+\frac{x^4}{4! } -\frac{x^6}{6! }+ \cdots}$

$\displaystyle{\sin(x) = x - \frac{x^3}{3!}+\frac{x^5}{5! } -\frac{x^7}{7! } + \cdots}$

and adding the two terms together yields:

$\begin{aligned} cos(x)+i\,sin(x) & = (1-\frac{x^2}{2!}+\frac{x^4}{4! } - \cdots) + i (x - \frac{x^3}{3! } + \frac{x^5}{5! } - \cdots) \\ & = 1 + ix + \frac{(ix)^2}{2! } + \frac{(ix)^3}{3! }+ \frac{(ix)^4}{4! } + \cdots \\ & = e^{ix} \end{aligned}$

This result is of fundamental importance in many fields of mathematics (for example, in complex analysis), physics and engineering.