The method of calculating future value for a single amount is relatively straightforward; it's just a matter of plugging numbers into an equation. The tough part is correctly identifying what information needs to be plugged in.
As previously discussed, there are four things that you need to know in order to find the FV:
- How does the interest accrue? Is it simple or compounding interest?
- Present Value
- Interest Rate
- Number of periods
Let's take one complex problem as an example:
On June 1, 2014, you will take out a $5000 loan for 8-years. The loan accrues interest at a rate of 3% per quarter. On January 1, 2015, you will take out another $5000, eight-year loan, with this one accruing 5% interest per year. The loan accrues interest on the principal only. What is the total future value of your loans on December 31, 2017?
First, the question is really two questions: What is the value of the first loan in 2017, and what is the value of the second in 2017? Once both values are found, simply add them together.
Let's talk about the first loan first. The present value is $5,000 on June 1, 2014. It is possible to find the value of the loan today, and then find it's value in 2017, but since the value is the same in 2017, it's okay to just imagine it is 2014 today. Next, we need to identify the interest rate. The problem says it's 3% per quarter, or 3% every three months. Since the problem doesn't say otherwise, we assume that the interest on this loan is compounded. That means we will use the formula in . Finally, we need to identify the number of periods. There are two and a half years between the inception of the loan and when we need the FV. But recall that the interest rate and periods must be in the same units. That means that the interest must either be converted to % per year, or one period must be one quarter. Let's take one period to be one quarter. That means there are 10 periods. Please note that we don't really care when the loan ends in this problem–we only care about the value of the loan on December 31, 2017.
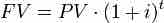
Compound Interest
Interest is paid at the total amount in the account, which may include interest earned in previous periods.
Next, we simply plug the numbers into . PV=5000, i=.03, and t=10. That gives us a FV of $6,719.58.
Now let's find the value of the second loan at December 31, 2017. Again, PV=$5000, but this time, pretend it is January 1, 2015. This time, the interest is 5% per year and it is explicitly stated to be simple interest. That means we use the formula in . January 31, 2017 is exactly two years from the January 1, 2015 and since the interest is measured per year, we can set t=2 years.
When we plug all of those numbers into , we find that FV=$5,500.00
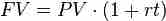
Simple Interest Formula
Simple interest is when interest is only paid on the amount you originally invested (the principal). You don't earn interest on interest you previously earned.
Since the problem asks for the total FV of the loans, we add $6,719.58 to $5,500.00, and get a total value of $12,219.58