Resistance and Resistivity

Resistance and Resistivity

Resistance is the electric property that impedes a current. A current flowing through a wire (or resistor) is like water flowing through a pipe, and the voltage drop across the wire is like the pressure drop which pushes water through the pipe. Resistance is proportional to how much pressure is required to achieve a given flow, while conductance is proportional to how much flow occurs for a given pressure. Conductance and resistance are reciprocals . The resistance of an object depends on its shape and the material of which it is composed. The cylindrical resistor is easy to analyze, and by so doing we can gain insight into the resistance of more complicated shapes. As you might expect, the cylinder's electric resistance R is directly proportional to its length L, similar to the resistance of a pipe to fluid flow. The longer the cylinder, the more collisions charges will make with its atoms. The greater the diameter of the cylinder, the more current it can carry (again, similar to the flow of fluid through a pipe). In fact, R is inversely proportional to the cylinder's cross-sectional area A.

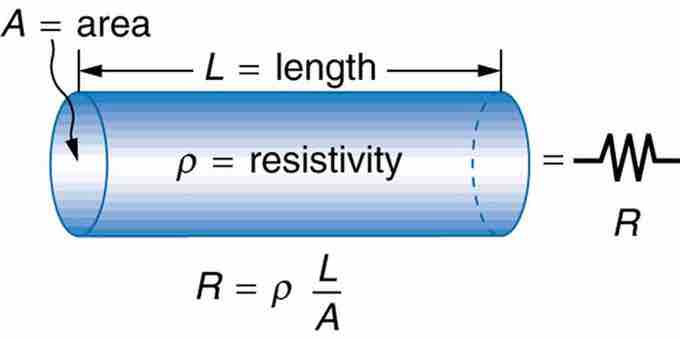
Cylindrical Resistor

A uniform cylinder of length L and cross-sectional area A. Its resistance to the flow of current is similar to the resistance posed by a pipe to fluid flow. The longer the cylinder, the greater its resistance. The larger its cross-sectional area A, the smaller its resistance.

As mentioned, for a given shape, the resistance depends on the material of which the object is composed. Different materials offer different resistance to the flow of charge. We define the resistivity ρ of a substance so that theresistanceR of an object is directly proportional to ρ. Resistivity ρ is an intrinsic property of a material, independent of its shape or size. In contrast, the resistance R is an extrinsic property that does depend on the size an shape of the resistor. (A similar intrinsic/extrinsic relation exists between heat capacity C and the specific heat c). Recall that an object whose resistance is proportional to the voltage and current is known as a resistor .

Typical Resistor

A typical axial-lead resistor.

What determines resistivity? The resistivity of different materials varies by an enormous amount. For example, the conductivity of teflon is about 1030 times lower than the conductivity of copper. Why is there such a difference? Loosely speaking, a metal has large numbers of "delocalized" electrons that are not stuck in any one place, but free to move across large distances, whereas in an insulator (like teflon), each electron is tightly bound to a single atom, and a great force is required to pull it away. Likewise, resistors range over many orders of magnitude. Some ceramic insulators, such as those used to support power lines, have resistances of 10¹² Ω or more. A dry person may have a hand-to-foot resistance of 10⁵ Ω, whereas the resistance of the human heart is about 10³ Ω. A meter-long piece of large-diameter copper wire may have a resistance of 10⁻⁵ Ω, and superconductors have no resistance at all (they are non-ohmic). The potential difference (voltage) seen across the network is the sum of those voltages, thus the total resistance (the series equivalent resistance) can be found as the sum of those resistances:

$R_{eq}=R_{1}+R_{2}+\cdots +R_{N}$.

As a special case, the resistance of N resistors connected in series, each of the same resistance R, is given by NR.Resistors in a parallel configuration are each subject to the same potential difference (voltage), however the currents through them add. Thus the equivalent resistance (Req) of the network can be computed:

$\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\cdots +\frac{1}{R_{N}}$.

The parallel equivalent resistance can be represented in equations by two vertical lines "||" (as in geometry) as a simplified notation. Occasionally two slashes "//" are used instead of "||", in case the keyboard or font lacks the vertical line symbol. For the case of two resistors in parallel, this can be calculated using:

$R_{eq}=R_{1}\parallel R_{2}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}$.

As a special case, the resistance of N resistors connected in parallel, each of the same resistance R, is given by R/N. A resistor network that is a combination of parallel and series connections can be broken up into smaller parts that are either one or the other, such as is shown in .

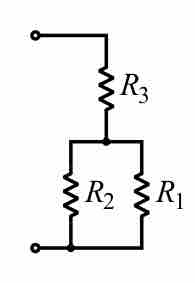
Resistor Network

In this combination circuit, the circuit can be broken up into a series component and a parallel component.

However, some complex networks of resistors cannot be resolved in this manner. These require a more sophisticated circuit analysis. One practical application of these relationships is that a non-standard value of resistance can generally be synthesized by connecting a number of standard values in series or parallel. This can also be used to obtain a resistance with a higher power rating than that of the individual resistors used. In the special case of N identical resistors all connected in series or all connected in parallel, the power rating of the individual resistors is thereby multiplied by N.