One of the most commonly used capacitors in industry and in the academic setting is the parallel-plate capacitor . This is a capacitor that includes two conductor plates, each connected to wires, separated from one another by a thin space. Between them can be a vacuum or a dielectric material, but not a conductor.
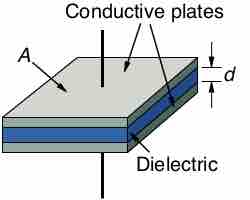
Parallel-Plate Capacitor
In a capacitor, the opposite plates take on opposite charges. The dielectric ensures that the charges are separated and do not transfer from one plate to the other.
The purpose of a capacitor is to store charge, and in a parallel-plate capacitor one plate will take on an excess of positive charge while the other becomes more negative.
Assuming the plates extend uniformly over an area of A and hold ± Q charge, their charge density is ±, where ρ=Q/A. Assuming that the dimensions of length and width for the plates are significantly greater than the distance (d) between them, the electric field (E) near the center of the plates can be calculated by:
Potential (V) between the plates can be calculated from the line integral of the electric field (E):
where z is the axis perpendicular to both plates. Through simplification and substitution, this integral can be changed to:
Given that capacitance is the quotient of charge and potential:
Accordingly, capacitance is greatest in devices with high permittivity, large plate area, and minimal separation between the plates.
The maximum energy (U) a capacitor can store can be calculated as a function of Ud, the dielectric strength per distance, as well as capacitor's voltage (V) at its breakdown limit (the maximum voltage before the dielectric ionizes and no longer operates as an insulator):