A Quantitative Interpretation of Motional EMF

An electromotive force (EMF) induced by motion relative to a magnetic field B is called a motional EMF. You might have noticed that motional EMF is very similar to the induced EMF caused by a changing magnetic field. In this Atom we see that they are indeed the same phenomenon, shown in different frame of reference.

Motional EMF

In the case where a conductor loop is moving into magnet shown in (a), magnetic force on a moving charge in the loop is given by $evB$ (Lorentz force, e: electron charge).

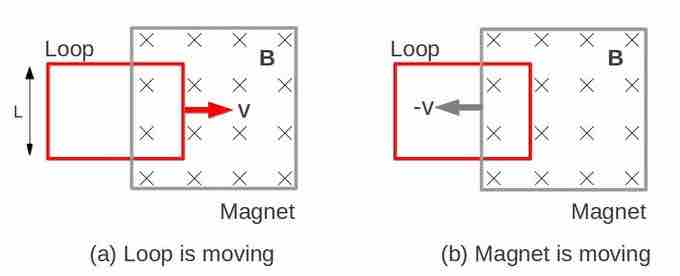
Conductor Loop Moving Into a Magnet

(a) Motional EMF. The current loop is moving into a stationary magnet. The direction of the magnetic field is into the screen. (b) Induced EMF. Current loop is stationary, and the magnet is moving.

Due to the force, electrons will keep building up on one side (bottom end in the figure) until enough of an electric field opposing the motion of electrons is established across the rod, which is $eE$. Equating the two forces, we get $E = vB$.

Therefore, the motional EMF over the length L of the side of the loop is given by $\varepsilon_{motion} = vB \times L$ (Eq. 1), where L is the length of the object moving at speed v relative to the magnet.

Induced EMF

Since the rate of change of the magnetic flux passing through the loop is $B\frac{dA}{dt}$(A: area of the loop that magnetic field pass through), the induced EMF $\varepsilon_{induced} = BLv$ (Eq. 2).

Equivalence of the Motional and Induced EMF

From Eq. 1 and Eq. 2 we can confirm that motional and induced EMF yield the same result. In fact, the equivalence of the two phenomena is what triggered Albert Einstein to examine special relativity. In his seminal paper on special relativity published in 1905, Einstein begins by mentioning the equivalence of the two phenomena:

"...... for example, the reciprocal electrodynamic action of a magnet and a conductor. The observable phenomenon here depends only on the relative motion of the conductor and the magnet, whereas the customary view draws a sharp distinction between the two cases in which either the one or the other of these bodies is in motion. For if the magnet is in motion and the conductor at rest, there arises in the neighbourhood of the magnet an electric field with a certain definite energy , producing a current at the places where parts of the conductor are situated. But if the magnet is stationary and the conductor in motion, no electric field arises in the neighbourhood of the magnet. In the conductor, however, we find an electromotive force, to which in itself there is no corresponding energy, but which gives rise—assuming equality of relative motion in the two cases discussed—to electric currents of the same path and intensity as those produced by the electric forces in the former case. "