As seen in previous Atoms, any change in magnetic flux induces an electromotive force (EMF) opposing that change—a process known as induction. Motion is one of the major causes of induction. For example, a magnet moved toward a coil induces an EMF, and a coil moved toward a magnet produces a similar EMF. In this Atom, we concentrate on motion in a magnetic field that is stationary relative to the Earth, producing what is loosely called motional EMF.
Motional EMF
Consider the situation shown in . A rod is moved at a speed v along a pair of conducting rails separated by a distance ℓ in a uniform magnetic field B. The rails are stationary relative to B, and are connected to a stationary resistor R (the resistor could be anything from a light bulb to a voltmeter). Consider the area enclosed by the moving rod, rails and resistor. B is perpendicular to this area, and the area is increasing as the rod moves. Thus the magnetic flux enclosed by the rails, rod and resistor is increasing. When flux changes, an EMF is induced according to Faraday's law of induction.
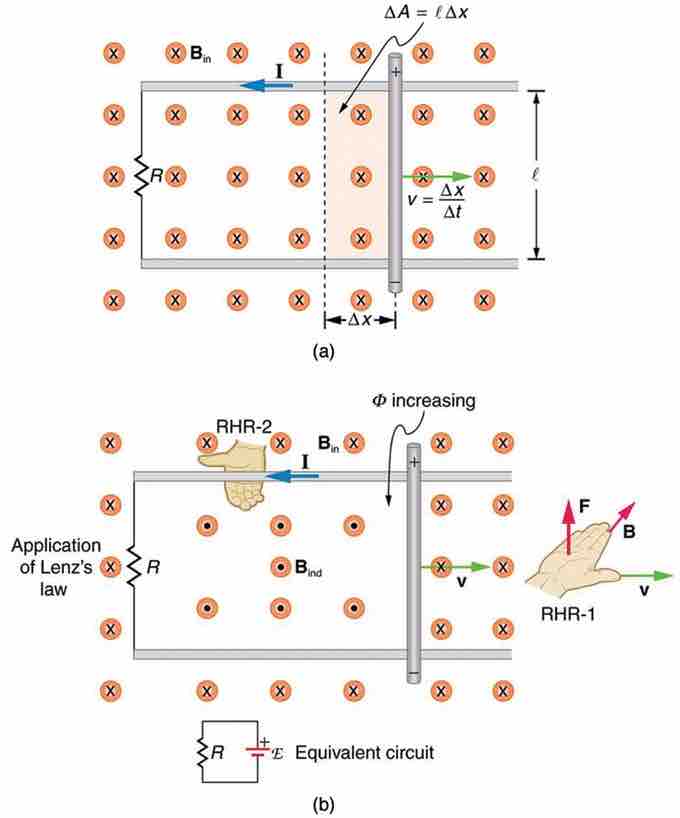
Motional EMF
(a) A motional emf=Bℓv is induced between the rails when this rod moves to the right in the uniform magnetic field. The magnetic field B is into the page, perpendicular to the moving rod and rails and, hence, to the area enclosed by them. (b) Lenz's law gives the directions of the induced field and current, and the polarity of the induced emf. Since the flux is increasing, the induced field is in the opposite direction, or out of the page. Right hand rule gives the current direction shown, and the polarity of the rod will drive such a current.
To find the magnitude of EMF induced along the moving rod, we use Faraday's law of induction without the sign:
In this equation, N=1 and the flux Φ=BAcosθ. We have θ=0º and cosθ=1, since B is perpendicular to A. Now Δ=Δ(BA)=BΔA, since B is uniform. Note that the area swept out by the rod is ΔA=ℓx. Entering these quantities into the expression for EMF yields:
To find the direction of the induced field, the direction of the current, and the polarity of the induced EMF we apply Lenz' law, as explained in Faraday's Law of Induction: Lenz' Law. As seen in Fig 1 (b), F lux is increasing, since the area enclosed is increasing. Thus the induced field must oppose the existing one and be out of the page. (The right hand rule requires that I be counterclockwise, which in turn means the top of the rod is positive, as shown. )
Electric Field vs. Magnetic Field
There are many connections between the electric force and the magnetic force. That a moving magnetic field produces an electric field (and conversely that a moving electric field produces a magnetic field) is part of the reason electric and magnetic forces are now considered as different manifestations of the same force (first noticed by Albert Einstein). This classic unification of electric and magnetic forces into what is called the electromagnetic force is the inspiration for contemporary efforts to unify other basic forces.