Elastic Collisions in Multiple Dimensions

Overview

As stated previously, there is conservation of total kinetic energy before and after an elastic collision. If an elastic collision occurs in two dimensions, the colliding masses can travel side to side after the collision (not just along the same line as in a one dimensional collision). The general approach to solving a two dimensional elastic collision problem is to choose a coordinate system in which the velocity components of the masses can be decomposed along perpendicular axes .

Example

In this example, we consider only point masses. These are structure-less particles that cannot spin or rotate. We will consider a case in which no outside forces are acting on the system, meaning that momentum is conserved. We will consider a situation in which one particle is initially at rest. This situation is illustrated in .

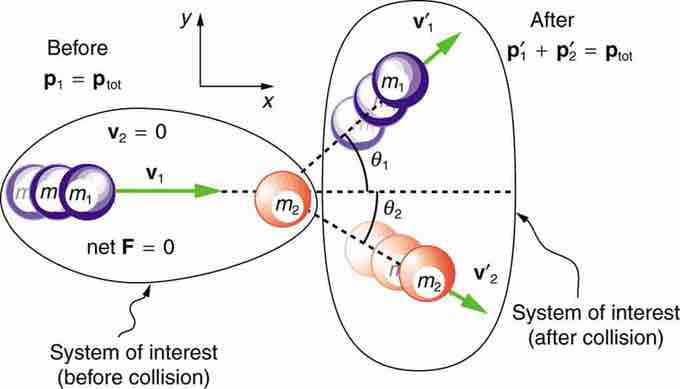
Illustration of Elastic Collision in Two Dimensions

In this illustration, we see the initial and final configurations of two masses that undergo an elastic collision in two dimensions.

By defining the x-axis to be along the direction of the incoming particle, we save ourselves time in breaking that velocity vector into its x- and y- components. Now let us consider conservation of momentum in the x direction:

$p_{1x}+p_{2x}=p{}'_{1x}+p{}'_{2x}$ (Eq. 1)

In Eq. 1, the initial momentum of the incoming particle is represented by p_{1x ,} the initial momentum of the stationary particle is represented by p_2x, the final momentum of the incoming particle is represented by p'_{1x .} and the final momentum of the initially stationary particle is represented by p'_2x.

We can expand Eq. 1 by taking into account that momentum is equal to the product of mass and velocity. Also, we know that p_2x = 0 because the initial velocity of the stationary particle is 0.

The components of velocities along the x-axis have the form $v \cdot cos \theta $, where θ is the angle between the velocity vector of the particle of interest and the x-axis.

Therefore:

$m_1v_1=m_1v{}'_1\cdot cos(\theta_1)+m_2v{'}_2\cdot cos(\theta_2)$ (Eq. 2)

The components of velocities along the y-axis have the form $v \cdot sin \theta $, where θ is the angle between the velocity vector of the particle of interest (denoted in the following equations by subscript 1 or 2) and the x-axis. We can apply conservation of momentum in the y-direction in a similar way to yield:

$0=m_1v{}'_1\cdot sin(\theta_1)+m_2v{'}_2\cdot sin(\theta_2)$ (Eq. 3)

In finding Eq. 3, it was taken into consideration that the incoming particle had no component of velocity along the y-axis.

Solving for Two Unknowns

Now we have gotten to a point where we have two equations, this means that we can solve for any two unknowns that we want. We also know that because the collision is elastic that there must be conservation of kinetic energy before and after the collision. This means that we may also write Eq. 4, which gives us three equations to solve for three unknowns:

$\frac{1}{2}m_1\cdot {v_{1}}^2+\frac{1}{2}m_2\cdot {v_{2}}^2=\frac{1}{2}m_1\cdot {v{}'_{1}}^2+\frac{1}{2}m_2\cdot {v{}'_{2}}^2$

The general approach to finding the defining equations for an n-dimensional elastic collision problem is to apply conservation of momentum in each of the n- dimensions. You can generate an additional equation by utilizing conservation of kinetic energy.