Circular Motion

Circular Motion of a Charged particle in a Magnetic Field

Magnetic forces can cause charged particles to move in circular or spiral paths. Particle accelerators keep protons following circular paths with magnetic force. Cosmic rays will follow spiral paths when encountering the magnetic field of astrophysical objects or planets (one example being Earth's magnetic field). The bubble chamber photograph in the figure below shows charged particles moving in such curved paths. The curved paths of charged particles in magnetic fields are the basis of a number of phenomena and can even be used analytically, such as in a mass spectrometer. shows the path traced by particles in a bubble chamber.

Bubble Chamber

Trails of bubbles are produced by high-energy charged particles moving through the superheated liquid hydrogen in this artist's rendition of a bubble chamber. There is a strong magnetic field perpendicular to the page that causes the curved paths of the particles. The radius of the path can be used to find the mass, charge, and energy of the particle.

So, does the magnetic force cause circular motion? Magnetic force is always perpendicular to velocity, so that it does no work on the charged particle. The particle's kinetic energy and speed thus remain constant. The direction of motion is affected, but not the speed. This is typical of uniform circular motion. The simplest case occurs when a charged particle moves perpendicular to a uniform B-field, such as shown in . (If this takes place in a vacuum, the magnetic field is the dominant factor determining the motion. ) Here, the magnetic force (Lorentz force) supplies the centripetal force

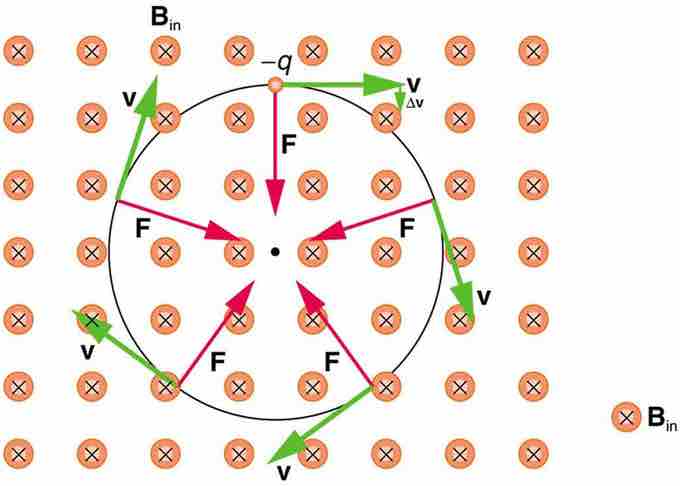
Circular Motion of Charged Particle in Magnetic Field

A negatively charged particle moves in the plane of the page in a region where the magnetic field is perpendicular into the page (represented by the small circles with x's—like the tails of arrows). The magnetic force is perpendicular to the velocity, and so velocity changes in direction but not magnitude. Uniform circular motion results.

$F_{c}=\frac{mv^{2}}{r}$.

Noting that

$sin\theta =1$

we see that

$F=qvB.$

The Lorentz magnetic force supplies the centripetal force, so these terms are equal:

$qvB=\frac{mv^{2}}{r}$

solving for r yields

$r=\frac{mv}{qB}$

Here, r, called the gyroradius or cyclotron radius, is the radius of curvature of the path of a charged particle with mass m and charge q, moving at a speed v perpendicular to a magnetic field of strength B. In other words, it is the radius of the circular motion of a charged particle in the presence of a uniform magnetic field. If the velocity is not perpendicular to the magnetic field, then v is the component of the velocity perpendicular to the field. The component of the velocity parallel to the field is unaffected, since the magnetic force is zero for motion parallel to the field. We'll explore the consequences of this case in a later section on spiral motion.

A particle experiencing circular motion due to a uniform magnetic field is termed to be in a cyclotron resonance. The term comes from the name of a cyclic particle accelerator called a cyclotron, showed in . The cyclotron frequency (or, equivalently, gyrofrequency) is the number of cycles a particle completes around its circular circuit every second and can be found by solving for v above and substituting in the circulation frequency so that

Cyclotron

A French cyclotron, produced in Zurich, Switzerland in 1937

$f=\frac{v}{2 \pi r}$

becomes

$f=\frac{qB}{2 \pi m}$

The cyclotron frequency is trivially given in radians per second by

$\omega=\frac{qB}{m}$.