Moving Observer

The Doppler effect is the apparent change in frequency of a wave when the observer and the source of the wave move relative to each other.

Learning Objective

Identify parameters required to calculate the frequency perceived by the observer moving towards the sound source

Key Points

When the object in motion moves towards the other, the frequency is increased because the time between successive sound waves is shortened. Therefore the pitch is higher.
When the object in motion moves away from the other, the frequency is decreased because the time between successive sound waves is lengthened. Therefor the pitch is lowered.
Unless the objects are in each other's direct path, you need to account for the angle they are at relative to each other. The following equation needs to be substituted for the 'movers' velocity. The angle used needs to be the angle from the line of sight of the observer to the sound source. $v_{radial}=v*cos\theta$.

Term

doppler effect
Apparent change in frequency of a wave when the observer and the source of the wave move relative to each other.

Full Text

In this atom, we are going to cover the Doppler effect , but specifically when the observer is the one in motion.

Sound and the Doppler Effect

This video introduces sound waves. The first video describes the basics of sound while the second video looks at the Doppler Effect.

When the observer moves toward an sound source, each successive wave is encountered sooner than the previous wave. Thus, it will take just a little less time for the observer to hear the next one. Since the time between waves is reduced, the frequency is increased. Similarly if the observer is moving away from the sound source, the frequency, and therefor pitch, is decreased. While the frequency will change whether the observer or sound source is moving, it is easier to show with the sound source as the one moving. This figure demonstrated the sound source moving:

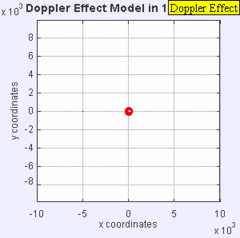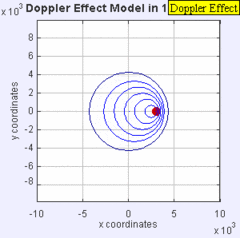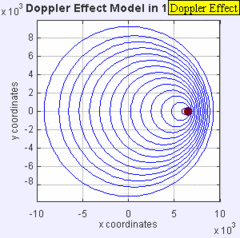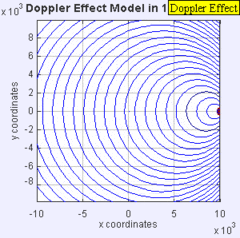
The Doppler Effect

The same sound source is radiating sound waves at a constant frequency in the same medium. However, now the sound source is moving to the right with a speed υs = 0.7 c (Mach 0.7). The wave-fronts are produced with the same frequency as before. However, since the source is moving, the centre of each new wavefront is now slightly displaced to the right. As a result, the wave-fronts begin to bunch up on the right side (in front of) and spread further apart on the left side (behind) of the source.

Unless the observer is moving directly towards the sound source, this angle needs to be taken into account when calculating the newly perceived frequency. Before we can start this calculation, we must know:

The original sound wave frequency, f₀
The velocity of the observer, v_r
The speed of sound in the air, or medium, c
The angle of the line of sight from the observer to the sound source, $\theta$

Although the sound waves are being emitted from the sound source at a uniform frequency, the observer is perceiving them differently. The equation for the perceived wave frequency is as follows:$f=\frac{c{\pm}v_{r,new}}{c}*f_0$And the equation for v_r, is:$v_{r,new}=v_r*cos\theta$If the observer is moving towards the sound source, you are going to use a plus sign in front of the observers velocity. If the observer is moving away from sound source, you are going to use a negative sign in front of the observers velocity.

[ edit ]

Prev Concept

Decibels

Moving Source

Next Concept