Circular Motion

An object in circular motion undergoes acceleration due to centripetal force in the direction of the center of rotation.

Learning Objective

Develop an understanding of uniform circular motion as an indicator for net external force

Key Points

An object that is undergoing circular motion has a velocity vector that is constantly changing direction.
The force that is needed to maintain circular motion points toward the center of the circular path. It is therefore known as the centripetal force.
The velocity of an object in circular motion is always tangent to the circle, and the centripetal force is always perpendicular to the velocity.

Terms

tangent
a straight line touching a curve at a single point without crossing it at that point
perpendicular
at or forming a right angle (to).

Example

Consider a space shuttle that orbits around the earth. Since the space shuttle is undergoing uniform circular motion, there must be a force that prevents the space shuttle from flying out of orbit. In this case, it is the gravitational force from the Earth. The relationship between the gravitational pull on the satellite from the Earth ($g'$) and the velocity of the space shuttle is: $mg'= \frac{mv^{2}}{r}$ where $m$ is the mass of the space shuttle, $v$ is the velocity at which it orbits around the earth, and $r$ is the radius of its orbit.

Full Text

Uniform circular motion describes the motion of an object along a circle or a circular arc at constant speed. It is the basic form of rotational motion in the same way that uniform linear motion is the basic form of translational motion. However, the two types of motion are different with respect to the force required to maintain the motion.

Let us consider Newton's first law of motion. It states that an object will maintain a constant velocity unless a net external force is applied. Therefore, uniform linear motion indicates the absence of a net external force. On the other hand, uniform circular motion requires that the velocity vector of an object constantly change direction. Since the velocity vector of the object is changing, an acceleration is occurring. Therefore, uniform circular motion indicates the presence of a net external force.

In uniform circular motion, the force is always perpendicular to the direction of the velocity. Since the direction of the velocity is continuously changing, the direction of the force must be as well.

The direction of the velocity along the circular trajectory is tangential. The perpendicular direction to the circular trajectory is, therefore, the radial direction. Therefore, the force (and therefore the acceleration) in uniform direction motion is in the radial direction. For this reason, acceleration in uniform circular motion is recognized to "seek the center" -- i.e., centripetal force.

The equation for the acceleration $a$ required to sustain uniform circular motion is:

$\displaystyle a =\frac{v^2}{r}$

where $m$ is the mass of the object, $v$ is the velocity of the object, and $r$ is the radius of the circle. Consequently, the net external force $F_{\text{net}}$ required to sustain circular motion is:

$\displaystyle F_{\text{net}}=\frac{m\cdot v^2}{r}$

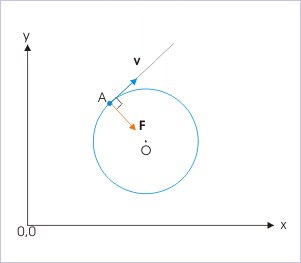
Uniform Circular Motion

In uniform circular motion, the centripetal force is perpendicular to the velocity. The centripetal force points toward the center of the circle, keeping the object on the circular track.

[ edit ]

Prev Concept

Connected Objects

Kinematics of UCM

Next Concept