Thin Film Interference
This is a phenomenon that occurs when incident rays reflected by the upper and lower boundaries of a thin film interfere with one another and form a new wave. A material is considered to be a thin film if its thickness is in the sub-nanometer to micron range, e.g. a soap bubble. Studying the new wave can shed light on properties of the film, such as thickness or refractive index. Interference effects are most prominent when the light interacts with something that has a size similar to its own wavelength. The thickness of a thin film is a few times smaller than the wavelength of the light, λ. Color is indirectly associated with wavelength. The interference ratio of wavelength to size of the object causes the appearance of colors.
Examples of Thin Film Interference
You have probably witnessed thin film interference in your every day life and just not realized it. Whenever you see the bright, rainbow like colors in oil floating in water, shown in , this is thin film interference. The colors that appear in bubbles that kids play with are also a result of thin film interference. Thin film interference can have commercial applications, such as anti-reflection coatings and optical filters.

Thin Film Interference in Oil
Thin film interference can be seen in this oil slick.
How it Works
shows a diagram of how thin film interference works. As light strikes the surface of a film it is either transmitted or reflected at the upper surface. Light that is transmitted reaches the bottom surface and may once again be transmitted or reflected. The light reflected from the upper and lower surfaces will interfere. The degree of constructive or destructive interference between the two light waves is dependent upon the difference in their phase. This difference is dependent upon the thickness of the film layer, the refractive index of the film, and the angle of incidence of the original wave on the film. Additionally, a phase shift of 180° or
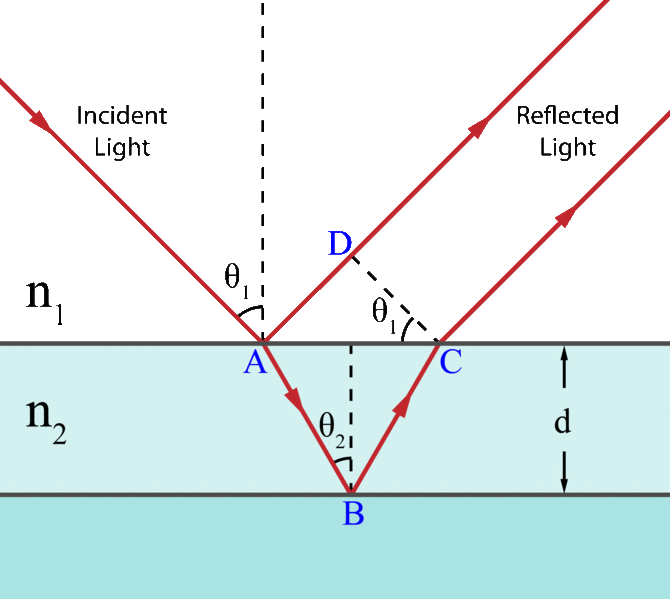
Light on a Thin Film
Light incident on a thin film. Demonstration of the optical path length difference for light reflected from the upper and lower boundaries.
Interference will be constructive if the optical path difference is equal to an integer multiple of the wavelength of light:
where