Polynomial Regression

Polynomial Regression

Polynomial regression is a higher order form of linear regression in which the relationship between the independent variable $x$ and the dependent variable $y$ is modeled as an $n$^th order polynomial. Polynomial regression fits a nonlinear relationship between the value of $x$ and the corresponding conditional mean of $y$, denoted $E(y\ | \ x)$, and has been used to describe nonlinear phenomena such as the growth rate of tissues, the distribution of carbon isotopes in lake sediments, and the progression of disease epidemics. Although polynomial regression fits a nonlinear model to the data, as a statistical estimation problem it is linear, in the sense that the regression function $E(y\ | \ x)$ is linear in the unknown parameters that are estimated from the data. For this reason, polynomial regression is considered to be a special case of multiple linear regression.

History

Polynomial regression models are usually fit using the method of least-squares. The least-squares method minimizes the variance of the unbiased estimators of the coefficients, under the conditions of the Gauss–Markov theorem. The least-squares method was published in 1805 by Legendre and in 1809 by Gauss. The first design of an experiment for polynomial regression appeared in an 1815 paper of Gergonne. In the 20^th century, polynomial regression played an important role in the development of regression analysis, with a greater emphasis on issues of design and inference. More recently, the use of polynomial models has been complemented by other methods, with non-polynomial models having advantages for some classes of problems.

Interpretation

Although polynomial regression is technically a special case of multiple linear regression, the interpretation of a fitted polynomial regression model requires a somewhat different perspective. It is often difficult to interpret the individual coefficients in a polynomial regression fit, since the underlying monomials can be highly correlated. For example, $x$ and $x^2$ have correlation around 0.97 when $x$ is uniformly distributed on the interval $(0, 1)$. Although the correlation can be reduced by using orthogonal polynomials, it is generally more informative to consider the fitted regression function as a whole. Point-wise or simultaneous confidence bands can then be used to provide a sense of the uncertainty in the estimate of the regression function.

Alternative Approaches

Polynomial regression is one example of regression analysis using basis functions to model a functional relationship between two quantities. A drawback of polynomial bases is that the basis functions are "non-local," meaning that the fitted value of $y$ at a given value $x=x_0$ depends strongly on data values with $x$ far from $x_0$. In modern statistics, polynomial basis-functions are used along with new basis functions, such as splines, radial basis functions, and wavelets. These families of basis functions offer a more parsimonious fit for many types of data.

The goal of polynomial regression is to model a non-linear relationship between the independent and dependent variables (technically, between the independent variable and the conditional mean of the dependent variable). This is similar to the goal of non-parametric regression, which aims to capture non-linear regression relationships. Therefore, non-parametric regression approaches such as smoothing can be useful alternatives to polynomial regression. Some of these methods make use of a localized form of classical polynomial regression. An advantage of traditional polynomial regression is that the inferential framework of multiple regression can be used.

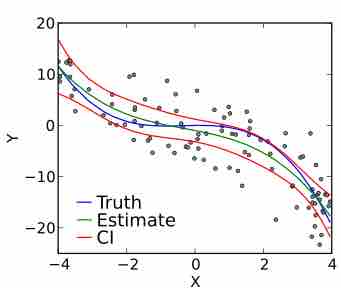
Polynomial Regression

A cubic polynomial regression fit to a simulated data set.