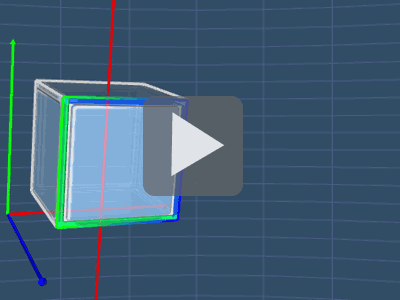
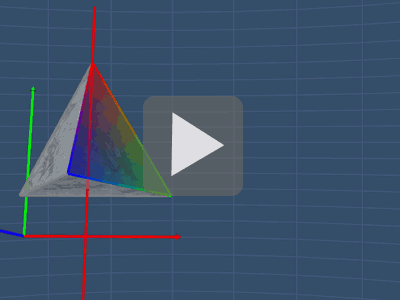
3D Rotation Symmetry - Cube and Tetrahedron

Lesson Objective

In this lesson, we will learn about rotation symmetry for a cube and tetrahedron.

About This Lesson

After familiarizing with the basics of rotational symmetry, we can now examine the rotational symmetry for 3-Dimensional objects.

In this lesson, we will see examine all the axes of rotational symmetry for a cube and tetrahedron.

CUBE TETRAHEDRON

You can proceed by reading the study tips first or watch the math video or try out the practice questions.

Study Tips

Tip #1

For 3D rotational symmetry, the ideas are basically the same as 2D Rotational symmetry.

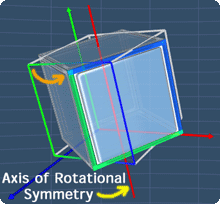
Looking at the picture, when we rotate the cube 360^o about the axis, notice that the cube will fit (i.e. match) itself for 4 times.

When this happens, the axis is called axis of rotational symmetry of order 4.

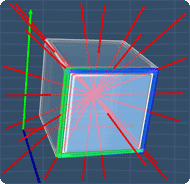
Tip #2

Next, the cube has a total of 13 axes of rotational symmetry. You can view them by watching the math video below.

Also, the step-by-step solution shown in the practice question will show you the pictures for these axes.

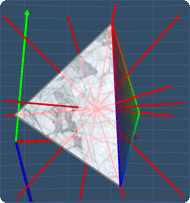
Tip #3

As for the tetrahedron, it has a total of 7 axes of rotational symmetry. You can view these axes in the math video below.

Also, the step-by-step solution shown in the practice question will show you all the pictures of these axes.

axes of rotational symmetry for a tetrahedron

Math Video

Rotation Symmetry for a Cube Video

!-->

Rotation Symmetry for a Tetrahedron Video

!-->

Math Videos Transcript

Transcript for Rotation Symmetry of a Cube and Tetrahedron

---CUBE---

00:00:02.180
This is a demonstration on rotational symmetry for a cube 

00:00:07.000
Now, consider this cube. When we rotate the cube about this axis for 360 degrees, we can see that, the cube matches itself for, one.. two... three... four times. 

00:00:25.210
With this, we can say that this axis, is the axis of rotational symmetry, of order 4.

00:00:33.050
Now, this cube has more than one axis of rotational symmetry. Let's explore them one by one.

00:00:40.100
This is the second axis of rotational symmetry. When we rotate the cube about this axis, we can see that the cube matches itself for one... two... three...four times. 

00:00:57.210
Hence, this axis of symmetry has order of 4. 

00:01:02.170
As for the third axis of rotational symmetry, it has order of, ...one... two... three... four.

00:01:14.240
For the fourth axis, this axis has order of...one...two...three.

00:01:26.230
For the fifth axis, this axis has order of...one...two...three.

00:01:39.030
For the sixth axis, this axis has order of...one...two...three.  

00:01:50.230
For the seventh axis, this axis has order of...one...two...three.

00:02:02.210
For the eighth axis, this axis has order of...one...two.

00:02:15.130
For the ninth axis, this axis has order of...one...two.

00:02:28.010
For the tenth axis, this axis has order of...one...two.

00:02:42.000
For the eleventh axis, this axis has order of...one...two.
00:02:54.150
For the twelfth axis, this axis has order of...one...two.

00:03:07.150
For the thirteen axis, this axis has order of...one...two.

00:03:20.230
Finally, we can see that this cube, has a total of 13 axis of rotational symmetry.

00:03:28.140
That is all for this video demonstration.



---TETRAHEDRON---

00:00:03.180
This is a demonstration on rotation symmetry for a tetrahedron. 

00:00:08.050
Now, consider this tetrahedron. When we rotate the tetrahedron about this axis for 360 degrees, we can see that, the tetrahedron matches itself for, one.. two... three.. times. 

00:00:29.130
With this, we can say that this axis, is the axis of rotational symmetry, of order 3.

00:00:36.240
Now, this tetrahedron has more than one axis of rotational symmetry. Let's explore them one by one.

00:00:44.000
This is the second axis of rotation symmetry. 

00:00:48.060
When we rotate the tetrahedron about this axis, we can see that the tetrahedron matches itself for one... two... three times. 

00:01:01.220
Hence, this axis of symmetry has order of 3. 

00:01:07.010
As for the third axis of rotation symmetry, this axis  has order of, one...two...three.

00:01:20.100
For the fourth axis, this axis has order of...one...two...three.

00:01:32.060
For the fifth axis, this axis has order of...one...two.
00:01:44.200
For the sixth axis, this axis has order of...one...two.

00:01:57.020
For the seventh axis, this axis has order of...one...two.

00:02:10.090
Finally, we can see that this tetrahedron has a total of 7 axis of rotational symmetry.

00:02:17.040
That is all for this demonstration.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on rotation symmetry or pick your choice of question below.

Question 1 on axis of rotational symmetry for a cube
Question 2 on axis of rotational symmetry for a tetrahedron

Return to Home Page