
Simplifying Algebraic Expressions - Removing Brackets
Lesson Objective
Learn how to remove brackets in algebraic
expressions.
About This Lesson
Algebraic expressions may contain brackets. In
order to simplify the expressions, you
may need to remove the brackets.
This lesson shows you the basics that you need to know when removing brackets.
This lesson shows you the basics that you need to know when removing brackets.
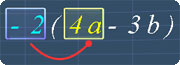
Study Tips
Tip #1
Remember to multiply all the terms in the
brackets with the term outside the brackets.
Tip #2
It is important understand why you are able to multiply
terms together in order to remove the brackets
in an expression.
Math Video
Math Video Transcript
Practice Questions & More
Multiple Choice Questions (MCQ)
Now, let's try some MCQ questions to understand
this lesson better.
You can start by going through the series of questions on simplifying algebraic expressions - removing brackets or pick your choice of question below.
You can start by going through the series of questions on simplifying algebraic expressions - removing brackets or pick your choice of question below.
- Question 1 on removing brackets
- Question 2 on removing brackets and simplifying