Recall that a linear system of equations consists of a set of two or more linear equations with the same variables. A linear system consisting of three equations in standard form arranged so that the variable x does not appear in any equation after the first and the variable y does not appear in any equation after the second is said to be in upper triangular formA linear system consisting of equations with three variables in standard form arranged so that the variable x does not appear after the first equation and the variable y does not appear after the second equation.. For example,

Notice that the system forms a triangle where each successive equation contains one less variable. In general,
If a linear system is in this form, we can easily solve for one of the variables and then back substitute to solve for the remaining variables.
Solve: .
Solution:
Recall that solutions to linear systems with two variables, if they exist, are ordered pairs (x, y). We can determine the y-value easily using the second equation.
Next, use the first equation and the fact that to find x.
Answer:
Solve: .
Solution:
Recall that solutions to linear systems with three variables, if they exist, are ordered triples (x, y, z). Use the second equation and the fact that to find y.
Next substitute y and z into the first equation.
Answer:
In this section the goal is to develop a technique that streamlines the process of solving linear systems. We begin by defining a matrixA rectangular array of numbers consisting of rows and columns., which is a rectangular array of numbers consisting of rows and columns. Given a linear system in standard form, we create a coefficient matrixThe matrix of coefficients of a linear system in standard form written as they appear lined up without the variables or operations. by writing the coefficients as they appear lined up without the variables or operations as follows.
The rows represent the coefficients in the equations and the columns represent the coefficients of each variable. Furthermore, if we include a column that represents the constants we obtain what is called an augmented matrixThe coefficient matrix with the column of constants included.. For a linear system with two variables,
And for a linear system with three variables we have
Note: The dashed vertical line provides visual separation between the coefficient matrix and the column of constants. In other algebra resources that you may encounter, this is sometimes omitted.
Construct the augmented matrix that corresponds to: .
Solution:
This system consists of two linear equations in standard form; therefore, the coefficients in the matrix appear as they do in the system.
Construct the augmented matrix that corresponds to: .
Solution:
Since the equations are given in standard form, the coefficients appear in the matrix as they do in the system.
A matrix is in upper triangular form if all elements below the leading nonzero element in each successive row are zero. For example,

Notice that the elements below the main diagonal are zero and the coefficients above form a triangular shape. In general,
This is important because in this section we outline a process by which certain operations can be made to produce an equivalent linear system in upper triangular form so that it can be solved by using back substitution. An overview of the process is outlined below:

Once the system is in upper triangular form, we can use back substitution to easily solve it. It is important to note that the augmented matrices presented here represent linear systems of equations in standard form.
The following elementary row operationsOperations that can be performed to obtain equivalent linear systems. result in augmented matrices that represent equivalent linear systems:
Note: These operations are consistent with the properties used in the elimination method.
To efficiently solve a system of linear equations first construct an augmented matrix. Then apply the appropriate elementary row operations to obtain an augmented matrix in upper triangular form. In this form, the equivalent linear system can easily be solved using back substitution. This process is called Gaussian eliminationSteps used to obtain an equivalent linear system in upper triangular form so that it can be solved using back substitution., named in honor of Carl Friedrich Gauss (1777–1855).
Figure 3.1

Carl Friedrich Gauss (Wikipedia)
The steps for solving a linear equation with two variables using Gaussian elimination are listed in the following example.
Solve using matrices and Gaussian elimination: .
Solution:
Ensure that the equations in the system are in standard form before beginning this process.
Step 1: Construct the corresponding augmented matrix.
Step 2: Apply the elementary row operations to obtain upper triangular form. In this case, we need only to eliminate the first element of the second row, −1. To do this, multiply the second row by 9 and add it to the first row.

Now use this to replace the second row.
This results in an augmented matrix in upper triangular form.
Step 3: Convert back to a linear system and solve using back substitution. In this example, we have
Solve the second equation for y,
Substitute this value for y into the first equation to find x,
Answer:
The steps for using Gaussian elimination to solve a linear equation with three variables are listed in the following example.
Solve using matrices and Gaussian elimination: .
Solution:
Ensure that the equations in the system are in standard form before beginning this process.
Step 1: Construct the corresponding augmented matrix.
Step 2: Apply the elementary row operations to obtain upper triangular form. We begin by eliminating the first element of the second row, 2 in this case. To do this multiply the first row by −2 and then add it to the second row.
Use this to replace the second row.
Next, eliminate the first element of the third row, 4 in this case, by multiplying the first row by −4 and adding it to the third row.
Use this to replace the third row.
This results in an augmented matrix where the elements below the first element of the first row are zero. Next eliminate the second element in the third row, in this case −9. Multiply the second row by −3 and add it to the third row.
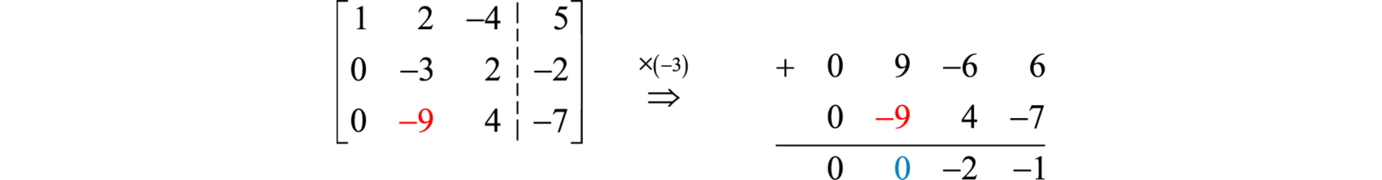
Use this to replace the third row and we can see that we have obtained a matrix in upper triangular form.
Step 3: Convert back to a linear system and solve using back substitution. In this example, we have
Answer: It is left to the reader to verify that the solution is .
Note: Typically, the work involved in replacing a row by multiplying and adding is done on the side using scratch paper.
Solve using matrices and Gaussian elimination: .
Solution:
We begin by converting the system to an augmented coefficient matrix.
The elementary row operations are streamlined if the leading nonzero element in a row is 1. For this reason, begin by interchanging row one and two.

Replace row two with the sum of −2 times row one and row two.

Replace row three with the sum of 4 times row one and row three.

Next divide row 3 by 15.

Interchange row three with row two.

Next replace row 3 with the sum of 5 times row two and row three.

This results in a matrix in upper triangular form. A matrix is in row echelon formA matrix in triangular form where the leading nonzero element of each row is 1. if it is in upper triangular form where the leading nonzero element of each row is 1. We can obtain this form by replacing row three with the results of dividing it by 9.

Convert to a system of linear equations and solve by back substitution.
Here y = 1 and . Substitute into the first equation to find x.
Answer: Therefore the solution is .
Technology note: Many modern calculators and computer algebra systems can perform Gaussian elimination. First you will need to find out how to enter a matrix. Then use the calculator’s functions to find row echelon form. You are encouraged to conduct some web research on this topic for your particular calculator model.
Recall that some consistent linear systems are dependent, that is, they have infinitely many solutions. And some linear systems have no simultaneous solution; they are inconsistent systems.
Solve using matrices and Gaussian elimination: .
Solution:
We begin by converting the system to an augmented coefficient matrix.
Replace row two with and replace row three with .
Replace row three with .
The last row indicates that this is a dependent system because converting the augmented matrix back to equations we have,
Note that the row of zeros corresponds to the following identity,
In this case, we can express the infinitely many solutions in terms of z. From the second row we have the following:
And from the first equation,
The solutions take the form where z is any real number.
Answer:
Dependent and inconsistent systems can be identified in an augmented coefficient matrix when the coefficients in one row are all zero.
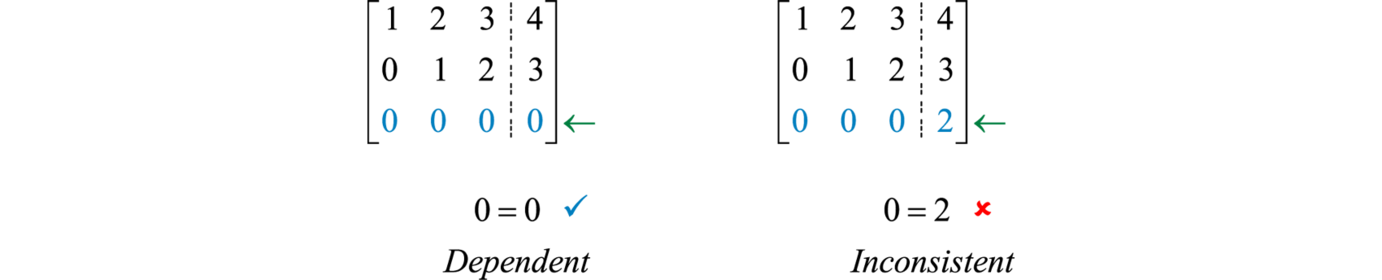
If a row of zeros has a corresponding constant of zero then the matrix represents a dependent system. If the constant is nonzero then the matrix represents an inconsistent system.
Solve using back substitution.
Construct the corresponding augmented matrix (do not solve).
Solve using matrices and Gaussian elimination.
Research and discuss the history of Gaussian Elimination. Who is credited for first developing this process? Post something that you found interesting relating to this story.
Research and discuss the history of modern matrix notation. Who is credited for the development? In what fields are they used today? Post your findings on the discussion board.
(−4, 0)
(0, 0)
(−8, 7, 3)
(−3, 5, 9)
(6, −2)
Ø
(0, 0)
(2, 3, 3)
(0, 1, 3)
(1, −1, 2)
Ø
(−7, −13, 7)
Ø
(2, −2, 1)
Answer may vary