Ir para o curso

Página 7: Propriedades dos divisores

/pt/multiplos-e-divisores/o-maximo-divisor-comum/content/

Propriedades dos divisores

Conhecer as propriedades dos divisores lhe ajudará a se familiarizar com eles e a realizar as operações com mais facilidade.

Todo número diferente de zero é divisor dele mesmo

Sempre que calculamos os divisores de um determinado número natural, veremos que o número em questão está na lista dos divisores. Por exemplo, os divisores de 20 são: Div(20)={1, 2, 4, 5, 10, 20} . Observe que o mesmo 20 faz parte da lista dos divisores de 20 , isto acontece com todos os números.

O motivo para que isto aconteça é o seguinte: dado um número a , entendemos que a=1xxa  ou seja, a está uma vez em a , e o resto da divisão adiva é zero. Lembre-se que são precisamente essas as condições que o definem como divisor.

Esta propriedade pode ser representada de várias formas:

  • Para todo número a diferente de zero, a divide a a: a|a .
  • Para todo número a diferente de zero   ainDiv(a)

Um é divisor de todos os números

Você já notou que quando calculamos os divisores de um número sempre aparece o um? Isso tem uma explicação: basta observar que para todo número a temos a=axx1 . Por exemplo, 5=5xx1 ou 9=9xx1 ou seja, um está a vezes em a , portanto 1|a .

Se um número é divisor de outros dois, também é da sua soma e da sua subtração

Usemos como exemplo os números 3, 15 e 9 .  3 é divisor de 15 e de 9 , e conforme esta propriedade também deve ser divisor de sua suma: 15+9=24, e de sua subtração: 15-9=6 .

Como podemos ver na imagem abaixo, o 3 faz parte do conjunto de divisores de 6 e de 24 .

Divisores de 6 e 24.

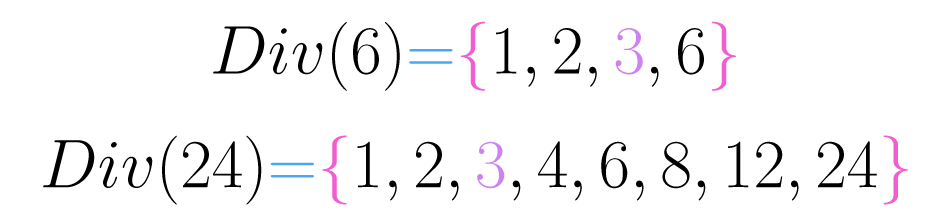
Podemos expressar esta propriedade assim: dados três números qualquer a, b e c , se a|b e a|c , então a|(b+c) e também a|(b-c) .

Propriedade transitiva

Definimos esta propriedade assim: se um número é divisor de outro e este outro de um terceiro, o primeiro é divisor do terceiro.

Por exemplo, 5 é divisor de 20 , e por sua vez 20 é divisor de 40 , a transitividade quer dizer que 5 deve ser divisor de 40 .

Divisores de 20 e 40.

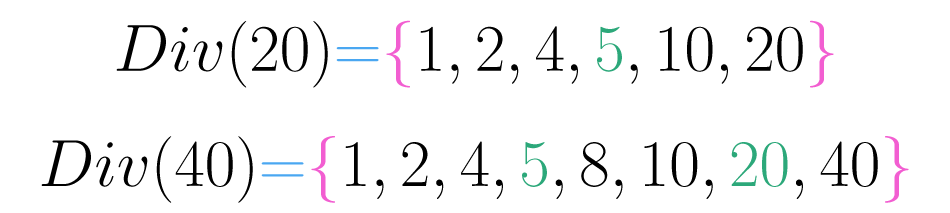
Observe que cada divisor de 20 também é divisor de 40 . Esta propriedade é expressada assim: dados três números qualquer a,b e c , se a|b e b|c então a|c .

/pt/multiplos-e-divisores/propriedades-do-maximo-divisor-comum/content/