
/pt/numeros-fracionarios/ampliacao-de-fracoes/content/
Simplificar frações lhe ajudará a fazer operações com mais facilidade:
Observe a seguinte situação: uma determinada pizzaria vende pedaços de um doze avos de uma pizza. Ana, que vai comprar para seus amigos, precisa de quinze pedaços. No entanto, no restaurante, que tem uma nova administração, agora os pedaços são de um quarto de pizza. Quantos pedaços Ana deve pedir agora?
Para saber quantos pedaços ela deve levar, Ana precisa encontrar uma fração equivalente: como cada pedaço é um doze avos e ela quer quinze, a fração de pizza que ela quer levar é quinze doze avos: . Mas agora, as novas porções são de um quarto de pizza, assim a fração de pizza que ela levará terá um denominador quatro: . Precisamos encontrar um número tal que:
Observe que para transformar o denominador doze em quatro, ele foi dividido em três. Desta forma, para encontrar o novo numerador, devemos fazer o mesmo, dividir o anterior em três: Se Ana levar porções ela pode ter certeza de que levará a mesma quantidade de pizza que precisa porque:
Sempre que numa fração, dividimos o numerador e o denominador pelo mesmo número, obtemos uma fração equivalente. Chamamos este processo de simplificação.
Para dividir o numerador e o denominador pelo mesmo número, ele deve ser um divisor comum dos dois. Por esta razão, o processo de simplificação para quando os números são primos relativos, ou seja, quando não têm mais divisores comuns do que Quando isso acontece, ou seja, quando uma fração não pode mais ser simplificada, dizemos que ela é irredutível.
Dada uma fração, podemos simplificar repetidamente até obter uma fração equivalente irredutível. O truque é dividir várias vezes por números primos, observe: simplifiquemos até obtermos sua fração equivalente mais simples:
Se alguém quiser chegar à expressão mínima de uma fração em uma única etapa, deve dividi-la pelo máximo divisor comum. No exemplo anterior , assim:
Observe que a decomposição prima de é , que são precisamente os números pelos quais dividimos no procedimento anterior.
Lembre-se que os números que estão no numerador multiplicam, enquanto os números que estão no denominador dividem. Podemos usar o fato de que a multiplicação e a divisão são operações opostas para simplificar de outra forma.
O que acontece se multiplicamos um número por dois e depois o dividimos por dois? A resposta é que o número original ficará igual, por exemplo: se primeiro multiplicamos o número seis por dois, obteremos: e se em seguida dividirmos esse resultado por dois: Podemos entender então que o dois multiplicando se anula com a que está dividindo e apenas permanece o Agora observe como podemos usar isso para simplificar:
As decomposições primas de e são e respectivamente, portanto:
Note que um dois, dois três e o sete estão ao mesmo tempo multiplicando e dividindo (para cima e para baixo), assim podemos anulá-los:
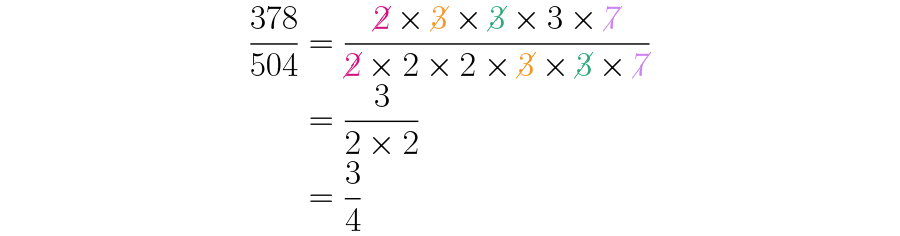
Assim, chegamos rapidamente à fração equivalente mais simples de .
/pt/numeros-fracionarios/numeros-mistos/content/