
/pt/os-conjuntos-matematicos/relacoes-entre-conjuntos-e-elementos/content/
Existem diferentes tipos de relações entre conjuntos. Nesta lição veremos a de continência.
Vamos definir como e os conjuntos das figuras abaixo representados pelo diagrama de Venn:
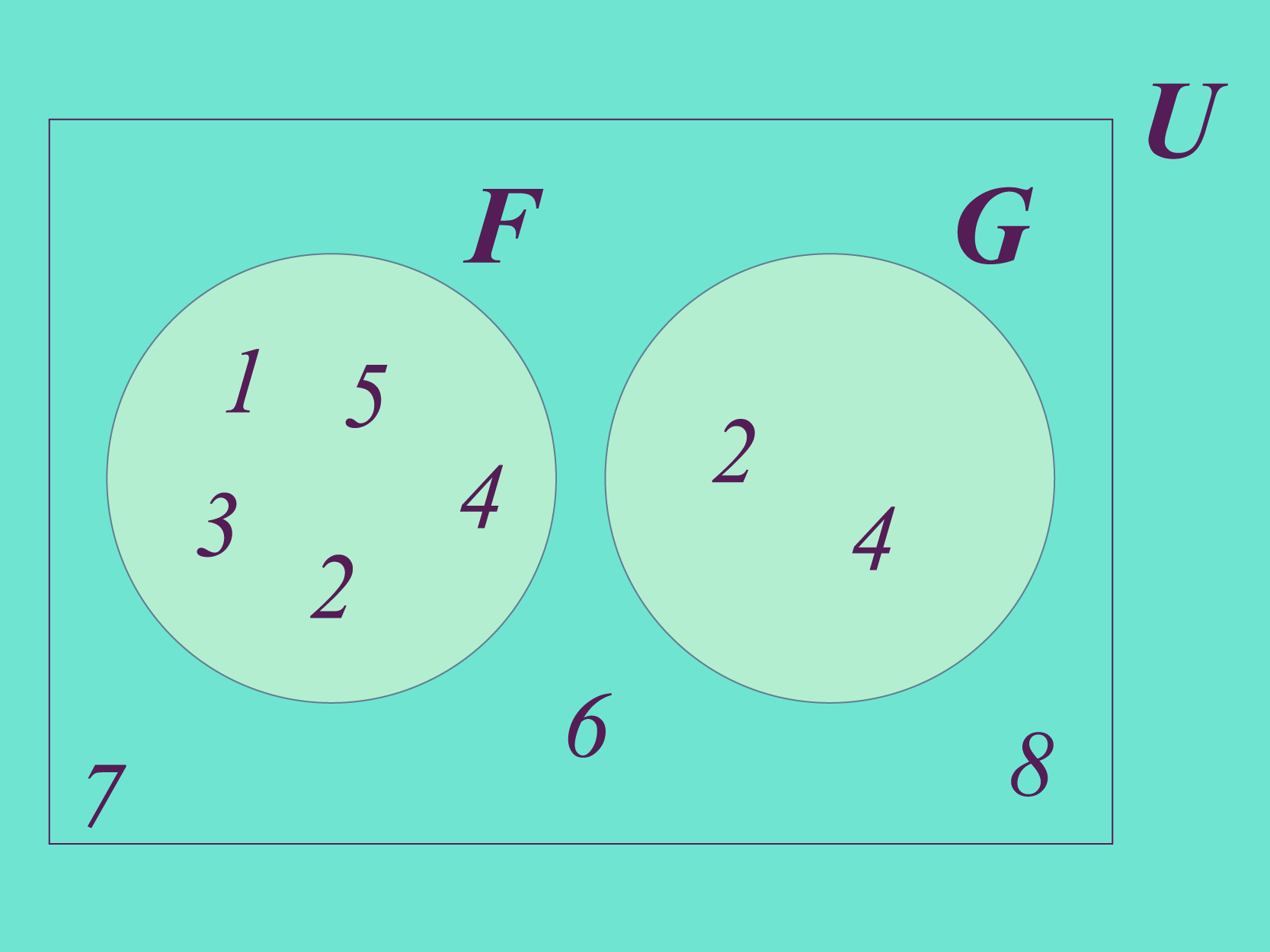
Como você pode observar, todo elemento que pertence ao conjunto , também pertence ao conjunto . Quando acontece esta situação, dizemos que um conjunto está contido no outro, ou que um é subconjunto do outro.
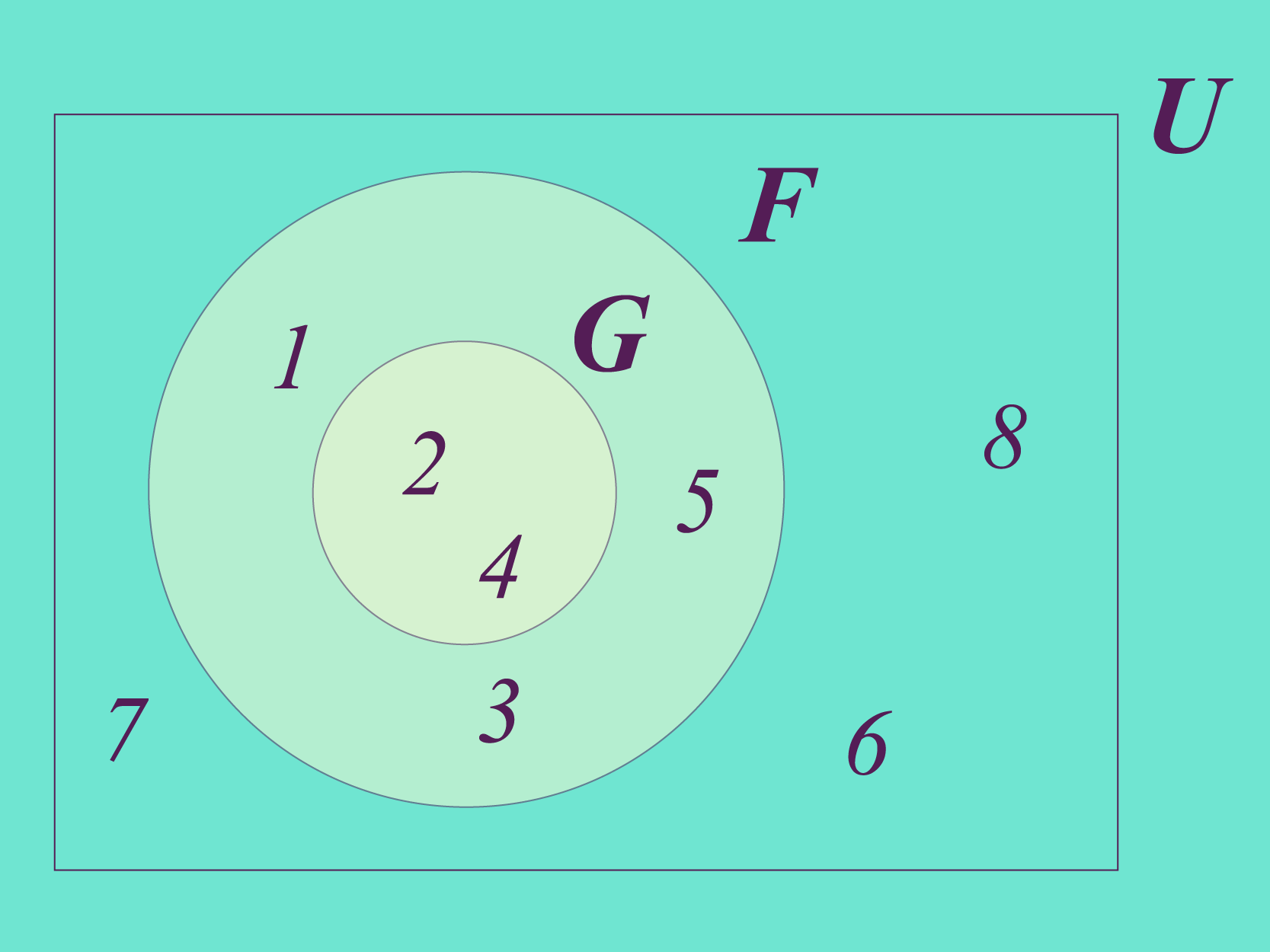
Neste caso, o está contido em , o que é igual a, é subconjunto de . A forma correta de representar a relação de continência, é desenhar um conjunto dentro do outro. Para o caso dos conjuntos e definidos anteriormente, a representação correta é como mostramos na figura de abaixo.
Também é possível representar de forma escrita a relação de continência entre conjuntos. Usamos o símbolo que está representado na parte esquerda da figura como o de Continência (contido em), e se queremos representar o Não contido em, usamos o mesmo símbolo com um traço no meio conforme mostrado na parte direita da figura.

Vamos definir os conjuntos , e . Você acha que existe alguma relação de continência entre estes conjuntos?
Lembre-se de que um conjunto está contido no outro se cada um dos seus elementos também pertence ao outro conjunto. Neste caso, cada elemento do conjunto pertence também ao conjunto , dizemos então que está contido em , ou que é subconjunto de .
Você acha que o conjunto está contido no conjunto ? Se observar com atenção, verá que há um elemento de que não está em . Portanto, não atende a condição de que cada elemento de também esteja em . Podemos afirmar então que, não está contido em , ou seja, que não é subconjunto de .
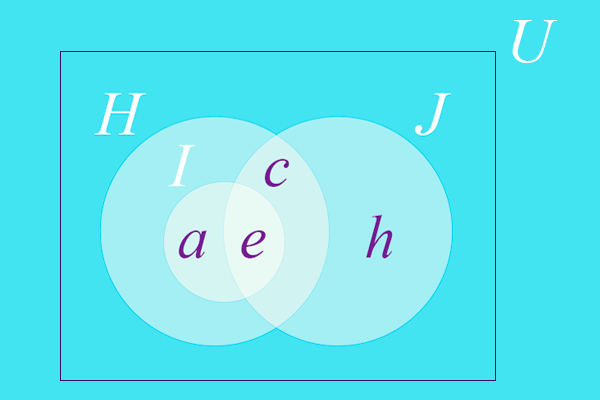
Para representar estas relações através do símbolo de continência, escrevemos da forma que você observa na figura abaixo. Estas expressões são lidas assim: " está contido em ", ou " é subconjunto de ", e " não está contido em ", ou " não é subconjunto de ".
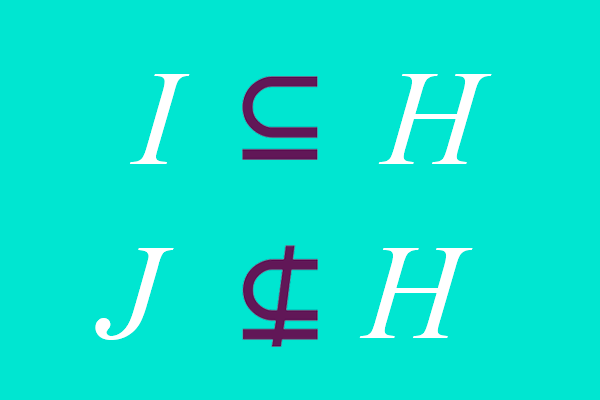
É importante saber representar graficamente a relação de continência entre os conjuntos. Para o caso dos conjuntos , e , podemos representá-los da seguinte forma:
/pt/os-conjuntos-matematicos/relacao-de-igualdade/content/