
/pt/os-numeros/ordem-no-conjunto-dos-numeros-inteiros/content/
Nem todos as quantidades podem ser representadas por números naturais ou inteiros, por isso veremos o que são números racionais.
Vamos considerar a seguinte situação: Três homens das cavernas vão em busca de frutas para colher. Eles passam o dia todo procurando e só encontram quatro melancias. Se quiserem repartir tudo em partes iguais quanto corresponderia a cada um deles?

Eles devem ficar com mais de uma melancia, porque eles são três e conseguiram colher mais do que esse número. Cada um teria duas se tivessem encontrado seis, mas não foi o caso. Assim, o número que representa a quantidade de melancia que está para cada um deles está entre e .
Você conhece algum número natural ou inteiro que representa o quanto terá cada um? Note que queremos representar o resultado da divisão de um número inteiro em partes iguais, neste caso quatro dividido por três. Precisamos de símbolos apropriados para representar essas divisões:
Suponhamos que e são dois números inteiros, ou seja, . Quando queremos distribuir a quantidade por em partes iguais, devemos escrever para representar cada uma dessas partes.
Vamos chamar de numerador o número de cima e de denominador o de baixo.
Voltando ao exemplo dos nossos amigos homens das cavernas, eles querem dividir quatro melancias em três partes iguais, representaremos a expressão assim , que podemos ler simplesmente como "quatro divido por três". Nestecaso o é o numerador e o o denominador.
Uma maneira de resolver o problemados três amigos é dar a todos uma melancia e dividir a que sobrou em três, assimcada um tem a porção que merece.
Agora temos os símbolos necessários para representar não só unidades inteiras, mas também podemos representar frações ou partes de unidades.
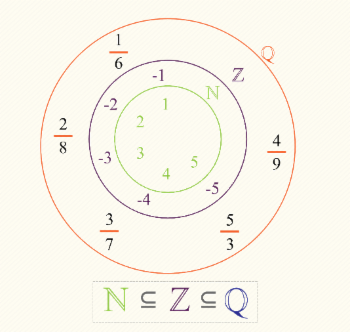
Chamaremos de conjunto de números racionais ou conjunto fracionários, o conjunto de todas as possíveis expressões do tipo , onde e são números inteiros e é diferente de zero. Representamos este conjunto por meio do símbolo .
Por exemplo, os números e fazem parte do conjunto dos números inteiros, portanto a expressão pertence ao conjunto dos fracionários, ou seja, .
Os números inteiros negativos também são considerados na hora de representar frações, as expressões , ou também pertencem a .
Podemos descrever o conjunto dos números racionais ou fracionários por compreensão assim:
A expressão anterior deve ser lido da seguinte forma: " é o conjunto das expressões , pois e são números inteiros e é diferente de zero".
/pt/os-numeros/algumas-propriedades-do-conjunto-dos-numeros-racionais/content/