
/pt/somar-e-subtrair/e-quando-nao-tem-parentesis/content/
Muitas vezes não será suficiente adicionar ou subtrair. Por isso é importante aprender como combinar a adição e a subtração para resolver certos problemas. Considere o seguinte:
Um ônibus vai pela cidade e em sua primeira parada recolhe passageiros, na segundo sobem e descem , já na terceira sobem e descem . Ao chegar no quarto ponto, quantos passageiros então no ônibus?
Para resolver este problema associamos algumas ações de adição e outra de subtração. Por exemplo, podemos associar que quando o ônibus pega passageiros a operação a ser realizada é a soma, e quando descem passageiros do ônibus associamos com a subtração. Então, quando traduzimos o problema em linguagem matemática temos: .
Podemos contar primeiramente o número de pessoas que sobem no ônibus: , e depois subtraímos o número de pessoas que saíram: . Desta forma obtemos a expressão: .
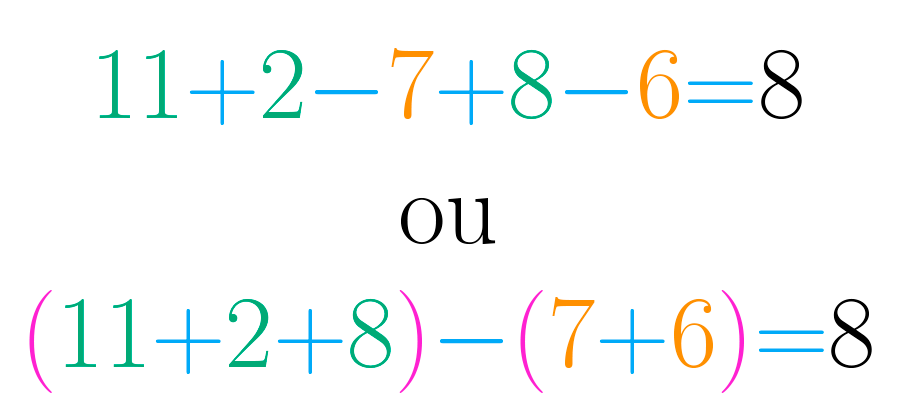
Note que estas duas expressões correspondem aos dois métodos explicados na página O uso dos parênteses. Resolvendo qualquer um destes cálculos chegaremos a conclusão de que no quarto ponto o ônibus terá pessoas.
Um caracol quer chegar até o topo de uma árvore e para fazer isso passa o dia inteiro subindo o seu tronco. À noite ele para e descansa mas seu peso faz com que ele baixe vários metros até o chão. Se durante o dia ele avança metros e a noite retrocede , depois de quatro dias completos, a quantos metros ele estará do chão?
Assim como no exemplo anterior, associamos certos dados a operação de soma e outros à operação de subtração. Desta forma faz sentido dizer que quando o caracol sobe devemos somar e que quando ele desce, subtrair. Assim, podemos demonstrar o que aconteceu nos quatro dias através da expressão:
O que está dentro de cada parêntesis representa um dia. Também seria correto expressarmos assim ou , todas estas expressões devem dar o mesmo resultado .

Podemos dizer desta forma que, ao terminar o quarto dia o caracol estará a metros acima do solo.
/pt/somar-e-subtrair/soma-e-subtracao-de-inteiros-na-reta/content/