
/pt/multiplos-e-divisores/propriedades-dos-divisores/content/
O máximo divisor comum ou , também possui propriedades úteis, veja:
Para entender esta afirmação vejamos como exemplo os números e . O máximo divisor comum de e é . Se multiplicamos estes dois números por três: e , o seu também é multiplicado por três. Assim o .
Para comprovar fazemos as decomposições primas de e . Os fatores comuns são e , assim que , como assegura esta propriedade.

O mesmo acontece se dividimos os números, por exemplo, e : . Se dividimos os números em , seu também é dividido em : .
Observe: . Assim se dividimos e em , os resultados devem ser coprimos. e . Na imagem abaixo podemos observar as decomposições primas destes dois números. Lembre que não há fatores primos comuns, o é igual a .
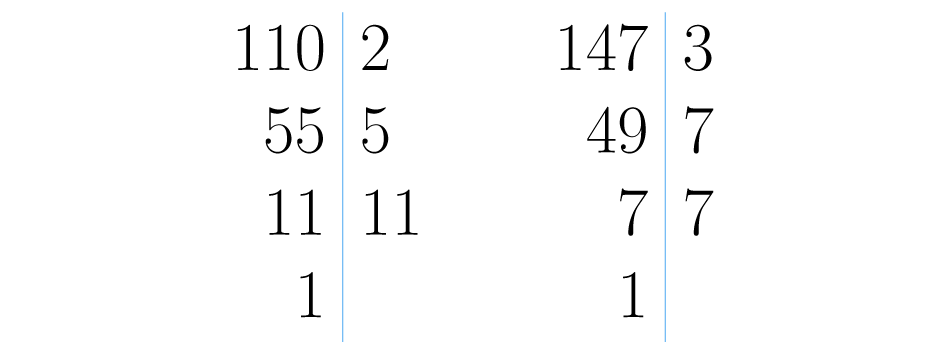
Como , podemos concluir que são primos relativos, assim como diz esta propriedade.
Usamos os números e como exemplo. é divisor de , esta propriedade diz que se calculamos seu ele deverá ser , vejamos: Quando realizamos as decomposições primas dos números, obtemos o resultado mostrado na imagem abaixo.

O será a multiplicação dos fatores primos comuns, neste caso .
/pt/multiplos-e-divisores/problemas-que-podem-ser-resolvidos-com-divisores/content/