
/pt/numeros-fracionarios/subtracao-de-fracoes-heterogeneas/content/
Se você quiser entender melhor a adição e a subtração de frações esta página foi feita para você.
Usamos fórmulas para a adição e subtração de frações heterogêneas porque quando temos denominadores diferentes, as frações representam tipos de objetos diferentes. Por exemplo, quando fazemos a soma , é fácil dizer que são , pois se trata de apenas um tipo de objetos: quartos. É como tentar adicionar cinco maçãs mais nove maçãs, onde obtemos a resposta: quatorze maçãs.
No entanto, quando as frações possuem denominadores diferentes, encontramos outro tipo de problema, isso porque estamos adicionando objetos diferentes, por exemplo, se ao adicionarmos três meios mais cinco terços e dissermos que a resposta é oito, não terá sentido porque não são nem oito meios e nem oito terços:
Para resolver este problema usamos as frações equivalentes com denominadores iguais, para que possamos somá-las mais facilmente. No interativo abaixo você pode ver o procedimento para efetuar essa soma.
Como você pode observar depois que são encontradas as frações equivalentes adequadas podemos fazer a soma de frações homogêneas, que é simplesmente contar quantas partes têm.
Observe que quando efetuamos o procedimento indicado pela fórmula para adicionar frações heterogêneas, obtemos os mesmos números, inclusive as frações e podem ser vistas na segunda linha deste procedimento:
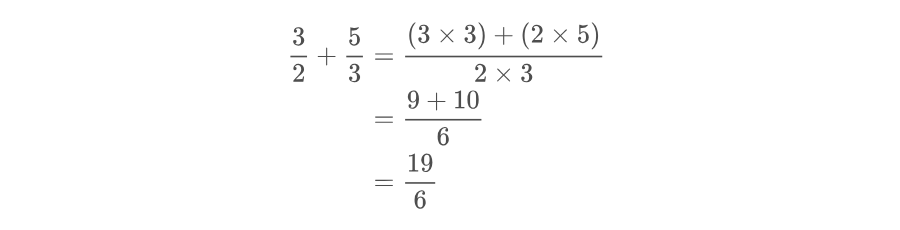
Uma boa forma de encontrar frações equivalentes rapidamente é transformando as frações de modo que tenham um denominador igual ao Mínimo Múltiplo Comum dos denominadores. Veja este exemplo com a soma .
Observe que se executamos o procedimento indicado pela fórmula obtemos a mesma resposta:
Para obter o mesmo resultado, foi necessário simplificar. A fórmula utilizada para adicionar frações é meramente uma maneira de encontrar frações equivalentes e no procedimento anterior as frações equivalentes encontradas foram: e .
/pt/numeros-fracionarios/problemas-com-somas-e-subtracoes-de-fracoes/content/