
/pt/numeros-fracionarios/fracoes-como-partes-da-unidade/content/
Além de serem interpretadas como partes das unidades, as frações também podem ser entendidas como partes de uma totalidade composta por muitas unidades.
Observe o seguinte exemplo: duas crianças juntaram dinheiro para comprar uma caixa de bombons com doze unidades. Como cada uma colaborou com diferentes valores, cada uma tem direito a partes diferentes. Para a primeira corresponde da caixa e para a segunda, . Com quantas bombons ficará cada criança?
Nesse caso, nossa unidade não é um único objeto como uma pizza, agora temos muitas unidades. Para calcular quanto corresponde à primeira criança, dividimos a unidade pelo número de partes iguais que indica o denominador e separamos a quantidade dessas partes indicada pelo numerador.
Assim como indica o três no denominador de , devemos dividir nossa unidade em três partes. Em seguida, como mostra o dois no numerador, pegamos duas dessas partes.
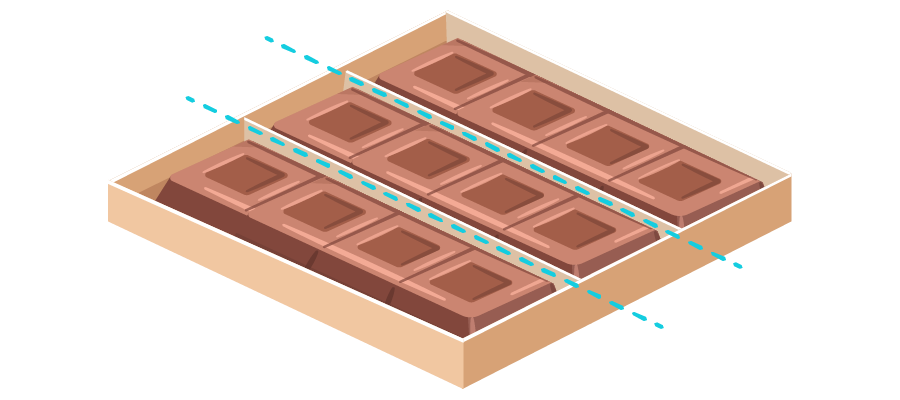
Como nossa unidade tem doze bombons, realizamos a divisão : e percebemos que, se dividirmos a caixa de doze em três partes iguais, cada parte será composta por quatro bombons. O dois no numerador de , indica que a primeira criança tem direito a duas dessas três partes, e como cada parte é quatro, ela ficará com bombons. Agora podemos observar porque afirmamos que os números que estão no numerador são multiplicados.
Descobrir a quantidade de bombons que pertencem à segundo criança agora é muito simples. Já dividimos nossa unidade de bombons em três partes iguais. O um que está na fração , nos diz que ela tem direitos a apenas uma dessas partes, assim, a segunda criança ficará com os quatro bombons que sobraram.
Ainda que nas próximas páginas explicaremos como funciona a soma de frações, este é o momento adequado para fazermos a seguinte observação: Veja que a soma de e da caixa, formam a totalidade. Em termos de operações, isso significa que . Desta vez, o símbolo não representa apenas uma unidade, como é de costume. Representa a totalidade que estamos dividindo, ou seja, a caixa de doze bombons.

As frações também podem ser usadas para estabelecer uma relação numérica entre as partes e o todo, observe:
Paula deve fazer uma prova que tem perguntas. Se das perguntas ela responder , qual fração da prova ela terá respondido?
Nesses casos entenderemos a expressão por extenso como a palavra 'de'. Assim, a expressão pode ser lida como " unidades de no total. Como Paula respondeu perguntas de um total de , podemos dizer que: 'treze de vinte', o que é igual: . Observemos outro exemplo:
Numa sala de aula tem alunos dos quais são meninos e são meninas, com quais frações do total podemos representar os meninos e as meninas da sala de aula?
Existem meninos dos estudantes, portanto a fração do total que os representa é . Da mesma forma é o total de meninas.
/pt/numeros-fracionarios/como-ler-as-fracoes/content/