
/pt/os-conjuntos-matematicos/conjuntos-equipotentes/content/
Para entender as relações entre os conjuntos, é necessário compreender primeiro como eles se relacionam com seus próprios elementos.
Para começar, devemos entender a relação entre os conjuntos e os elementos que o formam. Quando um objeto é um dos elementos de um conjunto, dizemos que ele pertence ao conjunto.
Como você pode ter percebido, é possível representar graficamente a relação de pertence por meio dos diagramas de Venn desenhando os elementos dentro de um círculo que representa o conjunto. Agora vejamos como representar esta relação por meio de símbolos matemáticos.
Usamos o símbolo que está na figura abaixo do lado esquerdo como o de pertence. Mas se queremos representar que um objeto não pertence a um determinado conjunto, colocamos o símbolo com um traço no meio, como mostrado no lado direito.

No exemplo abaixo, podemos ver que se trata de um conjunto unitário , que está formado pelo elemento . Os símbolos do lado direito representam de maneira escrita o mesmo que o diagrama de Venn.
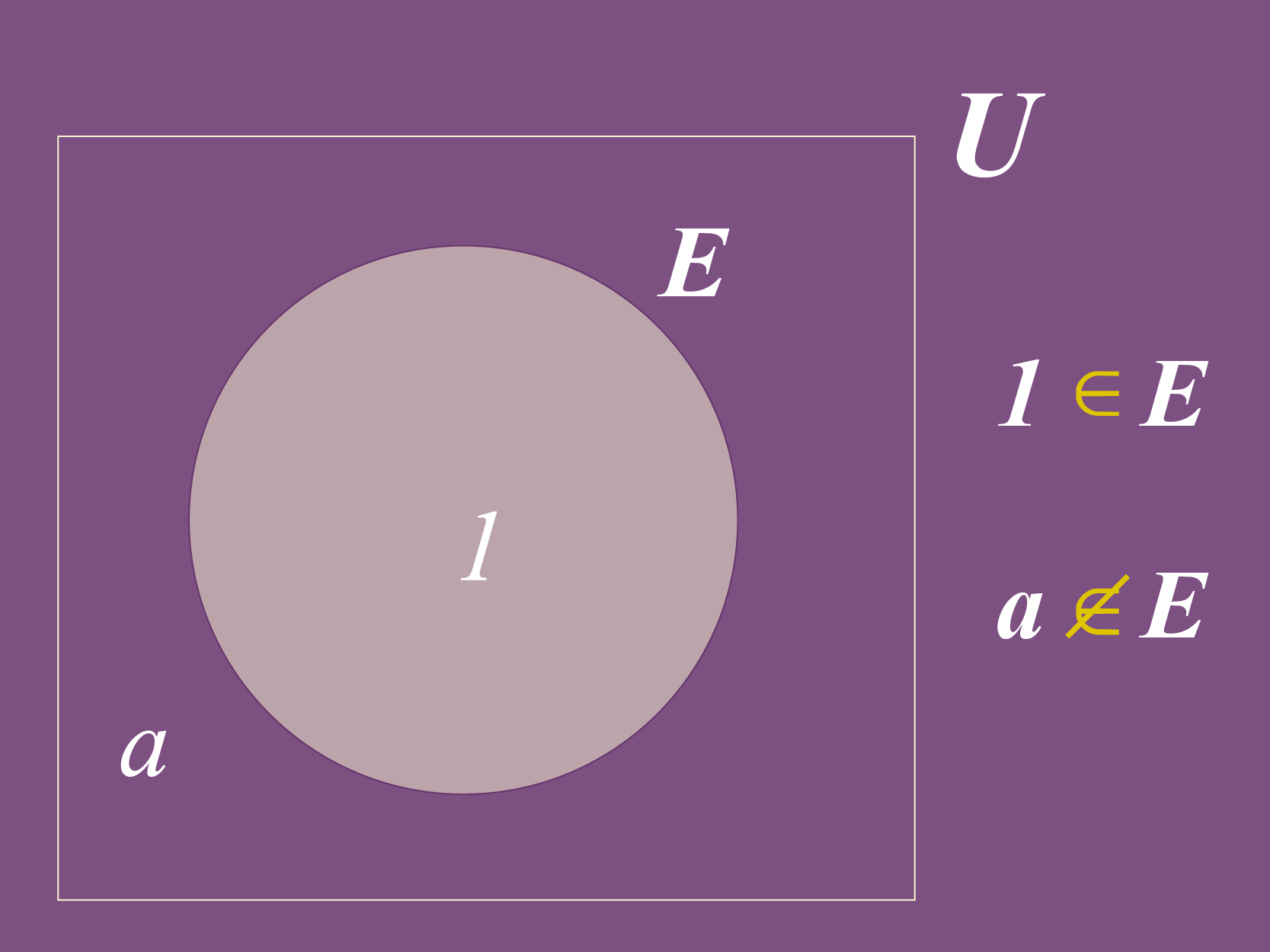
A expressão deve ser lida como " pertence a " ou " está em ". Perceba também que não está no conjunto , a expressão deve ser lida como " não pertence a " ou " não está em ".
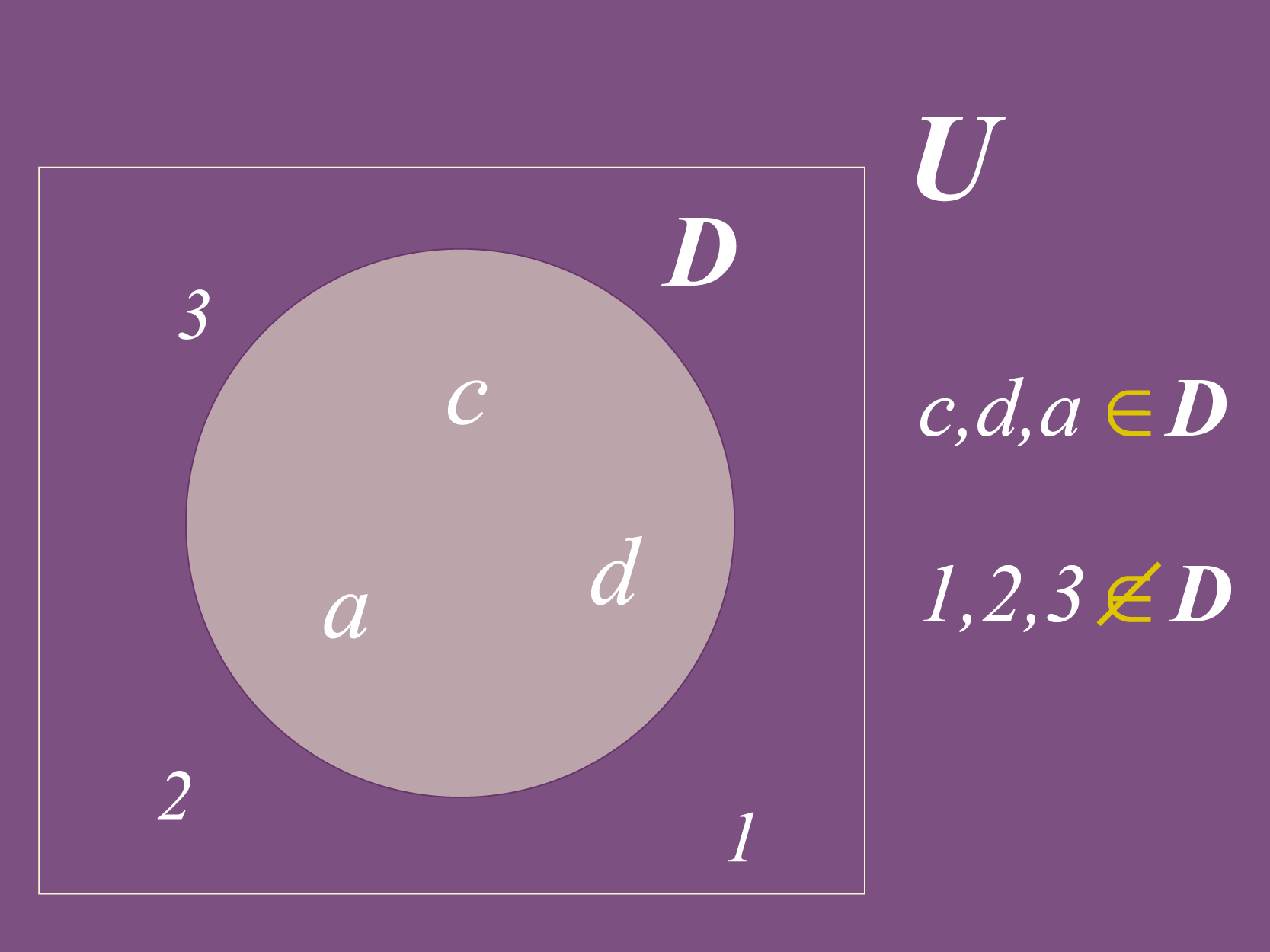
Veja este outro exemplo: na imagem baixo temos o conjunto formado pelos elementos , e . Para poder dizer que estes elementos pertencem ao conjunto , usaremos a seguinte expressão: "", que lemos: ", e pertencem a ". Os elementos , e não estão no conjunto ? Para representar esta situação podemos usar a expressão: "", que lemos como ", e não pertencem a ".
/pt/os-conjuntos-matematicos/relacao-de-contido-ou-nao-contido/content/