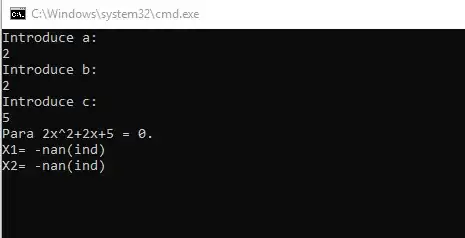
No se puede hacer la raíz cuadrada de un número negativo, eso es un valor indeterminado. Este es tu código:
x1 = (-b + sqrt((b*b) - (4 * a*c)))/(2*a);
x2 = (-b - sqrt((b*b) - (4 * a*c))) / (2 * a);
Éstos tus datos de entrada:
a = 2;
b = 2;
c = 5;
Substituyendo:
-
x1 = (-b + sqrt((b*b) - (4 * a*c)))/(2*a);
x2 = (-b - sqrt((b*b) - (4 * a*c))) / (2 * a);
-
x1 = (-2 + sqrt((2*2) - (4 * 2*5)))/(2*2);
x2 = (-2 - sqrt((2*2) - (4 * 2*5))) / (2 * 2);
-
x1 = (-2 + sqrt(( 4 ) - (4 * 10 )))/( 4 );
x2 = (-2 - sqrt(( 4 ) - (4 * 10 ))) / ( 4 );
-
x1 = (-2 + sqrt(( 4 ) - ( 40 )))/ 4 ;
x2 = (-2 - sqrt(( 4 ) - ( 40 ))) / 4 ;
-
x1 = (-2 + sqrt( -36 ))/ 4 ;
x2 = (-2 - sqrt( -36 )) / 4 ;
-
x1 = (-2 + indeterminado )/ 4 ;
x2 = (-2 - indeterminado ) / 4 ;
-
x1 = indeterminado / 4 ;
x2 = indeterminado / 4 ;
-
x1 = indeterminado ;
x2 = indeterminado ;
Ésto significa que la ecuación no tiene solución real para los valores facilitados. Sin embargo tiene solución imaginaria, utilizando números complejos (disponible en <complex>) puedes resolver tu problema:
double a, b, c;
cout << "Introduce a: \n";
cin >> a;
cout << "Introduce b: \n";
cin >> b;
cout << "Introduce c: \n";
cin >> c;
auto x1 = (-b + sqrt(complex((b*b) - (4 * a*c))))/(2*a);
auto x2 = (-b - sqrt(complex((b*b) - (4 * a*c)))) / (2 * a);
Esto resulta en la siguiente salida:
X1= (-0.5,1.5)
X2= (-0.5,-1.5)
Que es efectivamente la solución imaginaria a los datos de entrada. Puedes ver el código funcionando en Wandbox 三へ( へ՞ਊ ՞)へ ハッハッ.
El texto que te aparece -nan(ind) es un texto que depende de implementación. Está indicando que es un valor que no es un número (not a number) y que en concreto es una indeterminación de la ecuación.
Por cierto, ¿existe diferencia entre usar #include <cmath> y #include <math.h>? ¿es lo mismo o distintas versiones?
Esa pregunta ya ha sido respondida en este hilo.