/es/aplicaciones-de-la-matematica/los-numeros-binarios/content/

¿Cómo midió la tierra Eratóstenes?

Tal vez en alguna ocasión te hayas preguntado qué tan grande es el planeta Tierra.  ¿Cómo te las arreglarías si te retaran a medirla por tus propios esfuerzos?  Sí, por tus propios medios, esto implicaría que no puedes hacer uso de Google earth, GPS, o cualquier otra herramienta tecnológica ¿crees que es posible conseguirlo?  Pues resulta que un hombre muy inteligente lo consiguió, su nombre era Eratóstenes y lo hizo !hace más de 2200 años!  Si te quieres sorprender con el sencillo método que utilizó, aquí te lo explicamos.

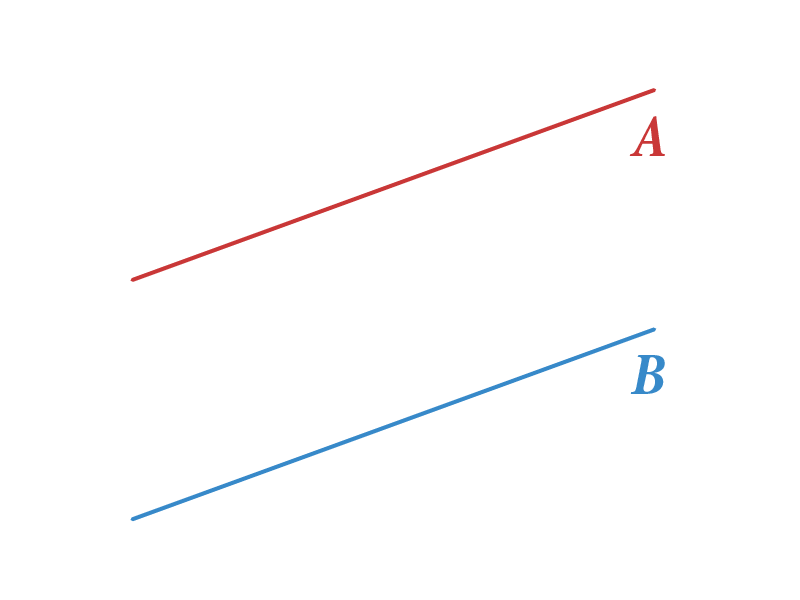
Empezaremos por repasar un sencillo concepto matemático.  Recordemos que dos rectas son paralelas si no se cortan en ningún punto, es decir, si tienen la misma inclinación.  En la imagen de la derecha puedes ver las rectas y , las cuales son paralelas.

Ahora trazaremos una recta que corte nuestras rectas paralelas, como resultado de esto se forman varios ángulos como se muestra en la figura:

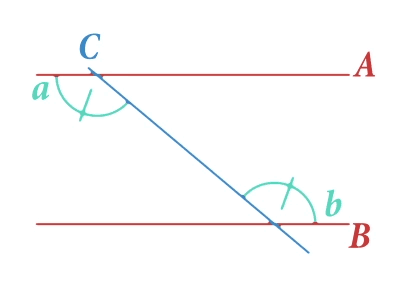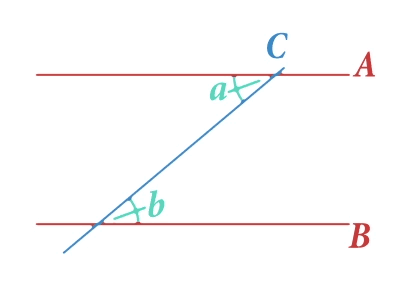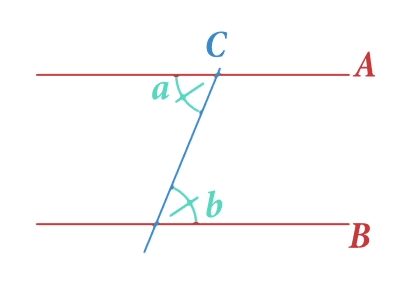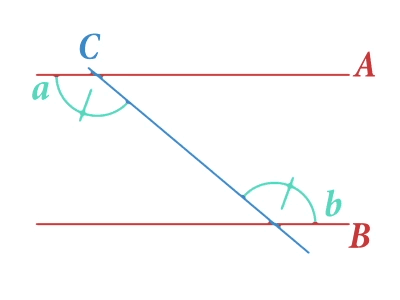
En la imagen anterior hemos destacado dos ángulos marcados con las letras y a los que llamaremos ángulos alternos internos.  Existe un principio geométrico que afirma la igualdad de estos dos ángulos.  Es decir, cualquiera que sea la inclinación de la recta , la medida de los ángulos y siempre será igual.  Esto nos ayudará a comprender cómo se las arregló Eratóstenes para llevar a cabo su cometido.  Veamos quién era este ilustre personaje y cómo lo hizo.

Eratóstenes nació en la ciudad griega Cirene, en la actual Libia, en el año 276 a.C.  Estudió en Alejandría y en Atenas, en donde se destacó por su gran capacidad intelectual.  Dominaba a la perfección disciplinas como la astronomía, matemáticas, poesía, geografía, historia y filosofía entre otras; era llamado beta (), la segunda letra del alfabeto griego, pues se consideraba que era el segundo mejor en todas estas disciplinas.  En 236 a.C. fue designado como director de la famosa biblioteca de Alejandría, cargo que ocupó hasta su muerte por inanición voluntaria, en el año 194 a.C.

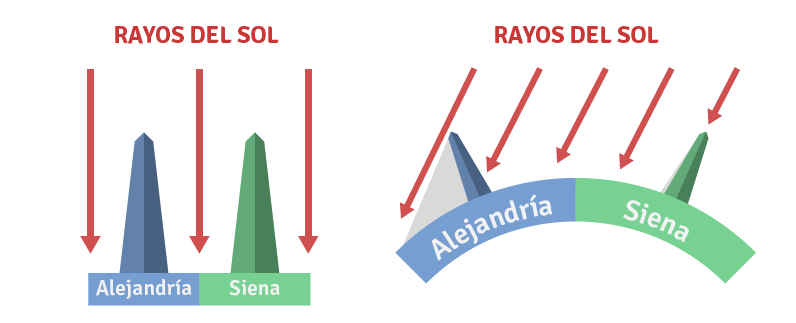
Mientras Eratóstenes estudiaba algunos pergaminos de la biblioteca, descubrió que en la antigua ciudad de Siena (hoy Asuán, en Egipto), en los solsticios de verano, a mediodía exactamente, no se proyectaban las sombras.  Sin embargo este fenómeno no se presentaba en Alejandría, pues allí las sombras sí se proyectaban a medio día en los solsticios.  Este hecho hizo pensar a Eratóstenes que la Tierra era redonda y no plana como se creía por entonces, pues si fuera plana, en Alejandría tampoco se deberían proyectar las sombras en ese momento:

Fue aquí donde Eratóstenes usó toda su creatividad: clavó un pequeño palito de la forma más vertical posible en la ciudad de Alejandría.  A pleno mediodía del solsticio de verano midió la sombra que este proyectaba como se muestra en la figura.

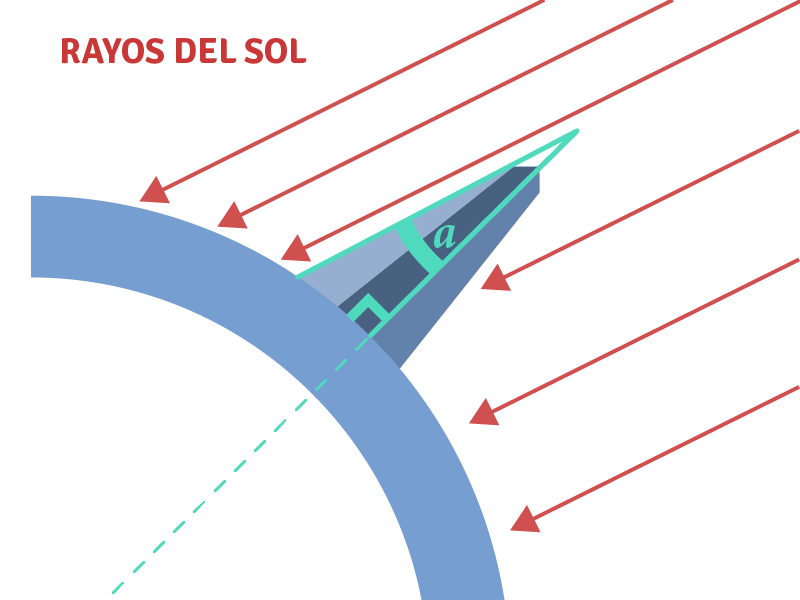
Como conocía la altura del palito que clavó y la longitud de la sombra, pudo determinar la medida del  el ángulo , en ese preciso instante.

Ahora bien, suponiendo, como lo hizo Eratóstenes, que el sol está lo suficientemente lejos de la Tierra, podemos asumir que los rayos del sol que llegan a Alejandría son paralelos a los rayos del sol que llegan a Siena.  Podemos representar esa situación de la siguiente manera:

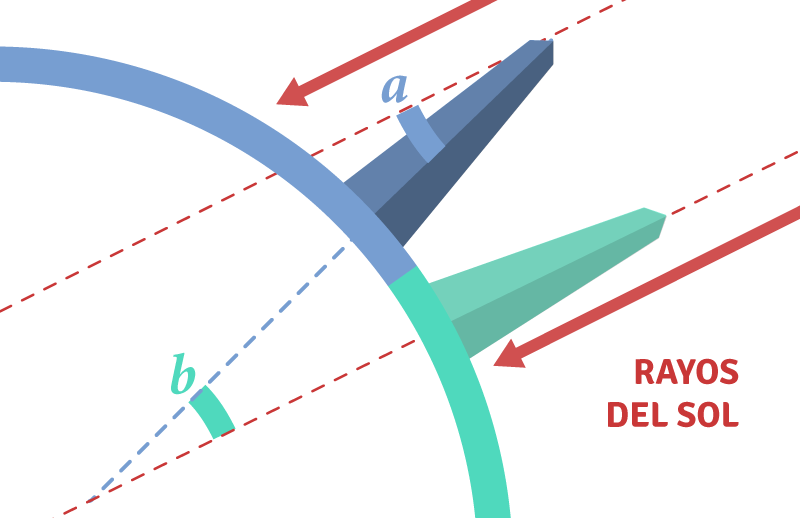
¿Recuerdas el principio geométrico que repasamos al comienzo del artículo?  Observa que las condiciones de paralelismo descritas se cumplen: los rayos del sol que pasan por Alejandría y Siena juegan el papel de las rectas paralelas. Además, podemos imaginar que el palito clavado por Eratóstenes dibuja una recta que corta las dos paralelas, haciendo que los ángulos y sean alternos internos, y por lo tanto tengan la misma medida.

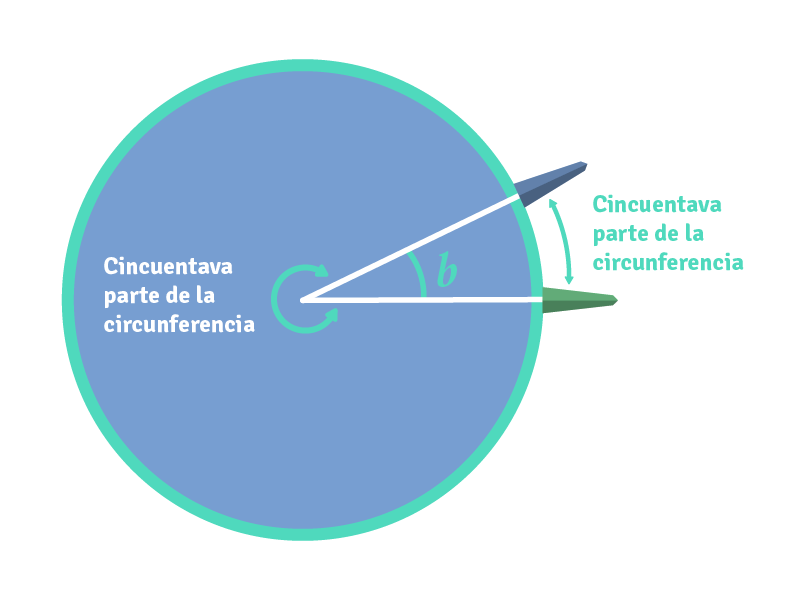
Como ya había calculado la medida del ángulo , tenía entonces también la del ángulo , que tiene como vértice el centro de la tierra, y cuyo arco es la distancia que hay desde la ciudad de Siena hasta Alejandría.  Cuando midió el ángulo (de igual medida que ), descubrió que es de aproximadamente , una cincuentava parte de la circunferencia completa, que mide (.

Por lo tanto, la distancia entre Alejandría y Siena debería ser también una cincuentava parte de la circunferencia de la Tierra.  Así que si se llegara a conocer la distancia entre Siena y Alejandría, sólo bastaría multiplicar esta por cincuenta y el resultado sería la medida de la circunferencia de la Tierra.

Con su propio dinero Eratóstenes pago para medir la distancia entre las dos ciudades.  Algunos dicen que a caravanas de comerciantes, otros que a compañías militares, otros que uno de sus sirvientes camino entre ellas contando cada paso.  Sea como fuere, Eratóstenes conocía, por lo menos aproximadamente, la distancia entre Alejandría y Siena.

Después de realizar los cálculos correspondientes, Eratóstenes aproximó la circunferencia de la Tierra en estadios, unidad de medida usada por ese entonces en Grecia.  En este punto existe una controversia, algunos historiadores aseguran que Eratóstenes usó el estadio ático-italiano, lo que se traduciría en una aproximación de km.  Otros dicen que usó el estadio egipcio, que daría una aproximación de km.  En cualquier caso son aproximaciones realmente buenas considerando los km que la ciencia actual acepta como circunferencia del planeta.  Un error prácticamente insignificante considerando la precariedad de los instrumentos de medida que usó para hacer sus estimaciones.

Conocí esta impresionante historia hace muchos años y siempre que puedo la comparto con mis estudiantes.  Creo que es un ejemplo vivo del poder del pensamiento humano y del alcance que tiene el hombre más allá de sus limitaciones físicas.  Eratóstenes no necesitó caminar un centímetro de la superficie terrestre y sin embargo la abarcó toda con el poder de su pensamiento.  ¡Y todo con un palito clavado en suelo!

/es/aplicaciones-de-la-matematica/sistema-internacional-de-unidades/content/