
/es/dividir/problemas-con-divisiones/content/
Las propiedades de las operaciones son herramientas muy útiles, pero si no se saben manejar pueden llevar a cometer errores. Aprende cuáles propiedades no puedes aplicar a una división.
Conmutar significa cambiar una cosa por otra. La propiedad conmutativa hace referencia al intercambio del orden de la operación. Es decir, si resulta lo mismo que Veamos a través de un ejemplo que la división no cumple esta propiedad.
Si realizamos obtenemos como resultado Por otra parte, si tratamos de resolver obtendremos que el resultado ni siquiera es un número entero, pues estamos dividiendo una sola unidad entera en dos partes iguales.
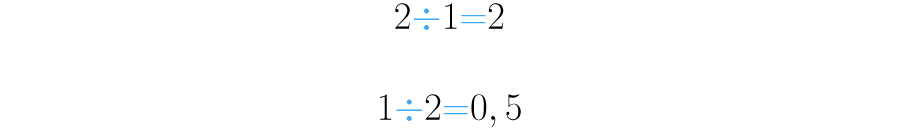
Se puede decir por lo tanto que dos dividido uno es diferente a uno dividido dos: y que la división no cumple la propiedad conmutativa.
La propiedad asociativa dice que cuando se tiene una expresión como es posible realizarla de dos formas: asociando los dos primeros números, o los dos últimos. Lo anterior quiere decir que, de cumplirse la propiedad asociativa, se debe tener Veamos si esto se cumple:
Resolvamos primero Operando en el orden que indican los paréntesis se realiza primero Luego se opera obteniendo el resultado final.
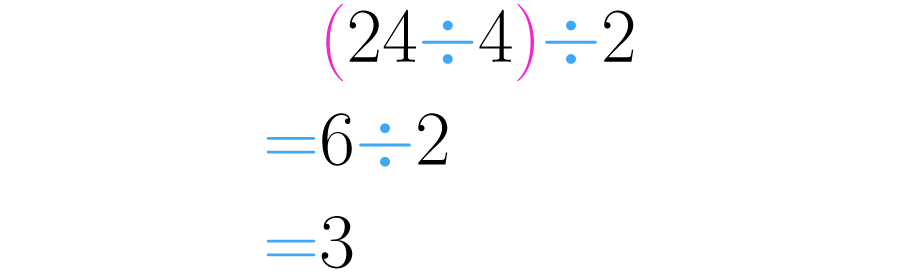
Por otra parte, resolviendo se empieza por que da como resultado Después se realiza así llegamos a la respuesta final.
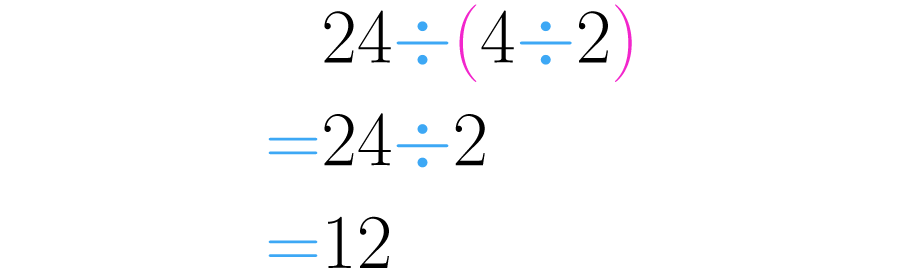
Como te puedes dar cuenta los resultados finales fueron distintos, de esta forma podemos concluir que la división no cumple la propiedad asociativa.
Fíjate que las siguientes divisiones: o , siempre tienen el mismo resultado: todas dan cero. Para entender por qué, interpretemos nuevamente la expresión .
Esta quiere decir que estamos repartiendo la cantidad en partes iguales. Así, la expresión , quiere decir que estamos distribuyendo cero unidades en siete partes iguales. ¿Cuántas unidades debe tener cada parte? ¡Precisamente cero!
Esto quiere decir que siempre que dividamos cero entre cualquier otro número obtendremos como resultado cero. Para generalizar esta idea podemos decir que si es cualquier número diferente de cero:
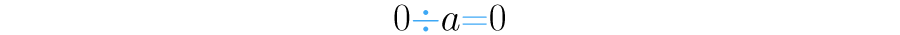
Pensemos ahora en el resultado de la expresión . ¿Cuántos grupos de cero puedes formar con tres unidades? ¿cero, uno, dos, tres, ninguno, o muchos?
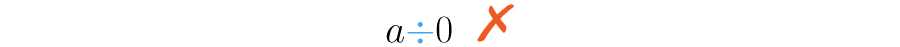
Tal vez hayas escuchado decir que la división y la multiplicación son operaciones inversas, ahora verás por qué esto es así.
Recuerda que el símbolo , usado para representar la multiplicación, es interpretado como “veces”. Así, cuando multiplicamos (por un natural), lo que hacemos es aumentar una cantidad.
La expresión significa “dos veces seis”. En este caso estamos aumentando la cantidad dos veces, es decir, estamos duplicando el seis: Por otra parte, cuando dividimos (en un natural) lo que estamos haciendo es distribuir una cantidad en varias partes iguales. La expresión representa cada una de las partes que resulta de repartir doce en dos partes iguales, se reduce pues la cantidad doce a la mitad:
En otras palabras: duplicar (multiplicar por dos) es lo contrario a partir por la mitad (dividir en dos), triplicar (multiplicar por tres) es lo contrario a partir en tres (dividir en tres), etc.
Primero dividimos seis en dos, obteniendo como resultado Después multiplicamos este resultado por dos, es decir, realizamos
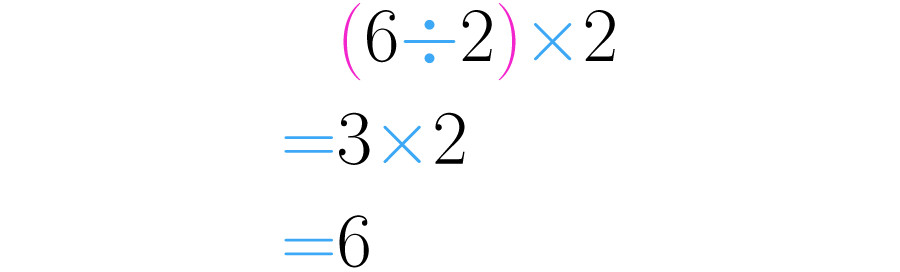
La respuesta final es el mismo número con el que se comenzó, el Ahora veamos que ocurre cuando se multiplica y luego se divide por el mismo número. Empecemos nuevamente por el seis:
Se realiza primero seis por dos, obteniendo como resultado. Luego dividamos este resultado por el mismo número que se multiplico antes, el dos:
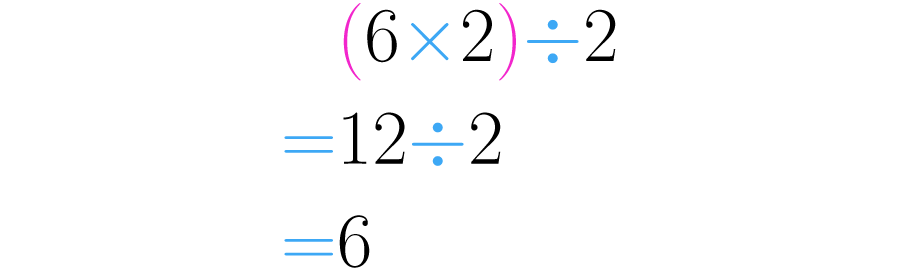
Como ves, en ambos casos el resultado fue el número inicial: el seis.
Si multiplicas y luego divides por el mismo número (o al contrario), las operaciones se cancelan. Por eso se dice que multiplicación y división son operaciones opuestas.
/es/dividir/division-con-suma-y-resta/content/