
/es/sumar-y-restar/y-cuando-no-hay-parentesis/content/
En muchas ocasiones no te bastará simplemente con solo sumar o solo restar. Es necesario aprender como combinar la suma y la resta para resolver determinados problemas. Analicemos el siguiente:
Un autobús se desplaza por la ciudad, en su primera parada recoge pasajeros, en la segunda se suben y se bajan , en la tercera se suben y se bajan . Al llegar a la cuarta parada, ¿cuántos pasajeros lleva el bus?
Para resolver este tipo de problemas se asocian algunas acciones con la suma y otras con la resta. Por ejemplo, podemos asociar que cuando el bus recoge pasajeros se realiza la operación sumar, y cuando de se bajan pasajeros del bus lo podemos asociar con la operación restar. Así, cuando traducimos el problema al lenguaje matemático obtenemos: .
También podemos contar primero el número de personas que se suben: y después restarle el número de personas que se bajan: . Obtenemos en ese caso la expresión: .
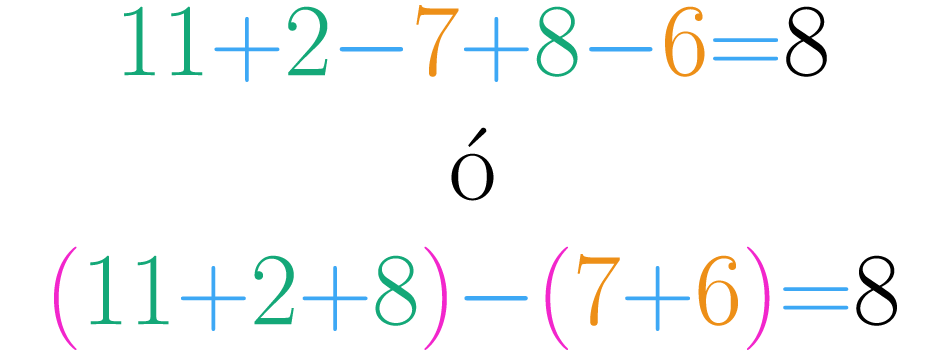
Nota que estas dos expresiones corresponden a los dos métodos explicados en la página uso de los paréntesis. Resolviendo cualquiera de estas obtenemos que al llegar a la cuarta parada en el autobús hay personas.
Un caracol quiere llegar a la copa de un árbol. Para hacerlo pasa el día entero subiendo su tallo, pero en la noche descansa y su peso hace que caiga varios metros hacia el suelo. Si en el día avanza metros y en la noche retrocede ¿al cabo de cuatro días completos, a cuantos metros estará del suelo?
Como en el ejemplo anterior asociamos ciertas acciones a la operación suma y otras a la operación resta. En este caso tiene sentido decir que cuando el caracol sube sumamos y cuando desciende restamos. Así, podemos contabilizar lo recorrido en los cuatro días por medio de la expresión: .
En donde cada paréntesis representa un día de recorrido. También sería correcto escribir o , todas estas expresiones deben dar el mismo resultado, que es .

Podemos decir entonces que al terminar el cuarto día el caracol se encontrará a metros del suelo.
/es/sumar-y-restar/suma-y-resta-de-enteros-en-la-recta/content/