
/es/sumar-y-restar/suma-y-resta-de-enteros-en-la-recta/content/
Al realizar sumas y restas te puedes encontrar con operaciones como la siguiente: que es una suma de dos números enteros negativos; o con algo así: que es la resta entre un número natural y un entero negativo. Cuando esto ocurre, se deben operar los signos como indica la siguiente tabla:
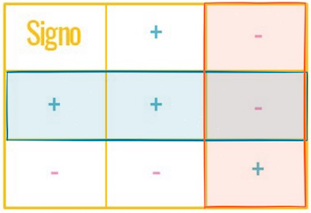
Cuando encontramos dos signos consecutivos, los reemplazamos por el signo que se encuentre en la intersección de la fila y la columna.
Por ejemplo, en la expresión encontramos dos signos seguidos: un más y un menos. Por lo tanto nos ubicamos en la fila del más y en la columna del menos, observa que en la intersección de estas dos hay un menos. Esto quiere decir que un más y un menos seguidos son lo mismo que un solo menos: . De esta forma . Nota que es igual si hay paréntesis: .
En muchos países se le conoce a la ley de signos como multiplicación de signos; sin embargo no es que sea como una multiplicación de números, simplemente es una forma de llamarle a estas relaciones.
En esos términos, siguiendo las indicaciones de la tabla ley de signos, podemos decir:
Otra forma de recordar los resultados anteriores es: multiplicación de signos iguales da como resultado más, de signos diferentes da menos:
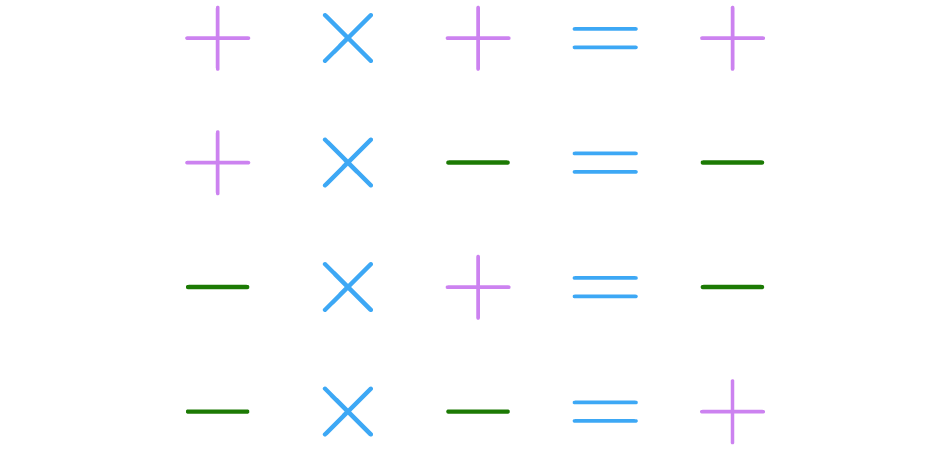
Supongamos que es un número natural mayor que cero: . Entonces la representación de en la recta numérica debe ser una flecha dirigida hacia la derecha.
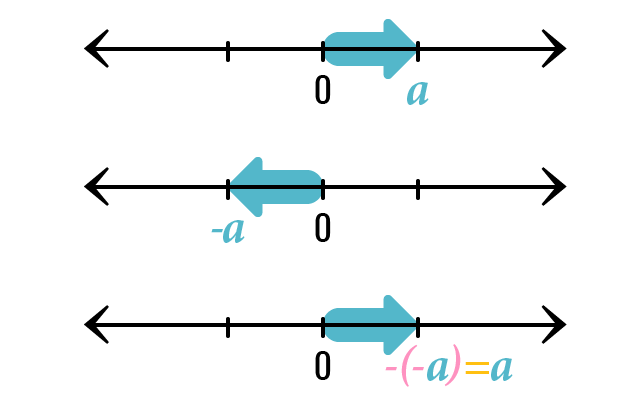
Sin embargo, si anteponemos un menos al número , obtenemos el número , que se representa por una flecha dirigida hacia la izquierda. Observa que si ponemos otro menos al : , gracias a la ley de signos obtenemos nuevamente pues según lo explicado arriba .
Podemos decir entonces que cuando un signo menos está antecediendo otro signo, cambia de sentido la flecha que representa el número en cuestión; mientras que el cuando el signo más antecede, no cambia el sentido de la misma.
/es/sumar-y-restar/simplificacion-de-expresiones-con-ley-de-signos/content/