Hyperpolarized carbon-13 MRI

Preclinical models

Hyperpolarized carbon-13 MRI is currently being developed as a potentially cost effective diagnostic and treatment progress tool in various cancers, including prostate cancer. Other potential uses include neuro-oncological applications such as the monitoring of real-time in vivo metabolic events.^[7]

Clinical trials

The majority of clinical studies utilizing ¹³C hyperpolarization are currently studying pyruvate metabolism in prostate cancer, testing reproducibility of the imaging data, as well as feasibility of acquiring time.^[8]

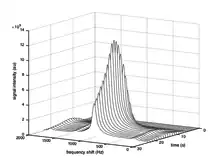
Spectroscopic imaging

Spectroscopic imaging techniques enable chemical information to be extracted from hyperpolarized carbon-13 MRI experiments. The distinct chemical shift associated with each metabolite can be exploited to probe the exchange of magnetization between pools corresponding to each of the metabolites.

Metabolite-selective excitation

Using techniques for simultaneous spatial and spectral selective excitation, RF pulses can be designed to perturb metabolites individually.^[9][10] This enables the encoding of metabolite-selective images without the need for spectroscopic imaging. This technique also allows different flip angles to be applied to each metabolite,^[11][12] which enables pulse sequences to be designed that make optimal use of the limited polarization available for imaging.^[13][14]

Two-species model with unidirectional flux

The simplest model of metabolic flux assumes unidirectional conversion of the injected substrate S to a product P. The rate of conversion is assumed to be governed by the reaction rate constant ${\displaystyle k_{{\ce {SP}}}}$

${\displaystyle {\ce {S->[{{} \atop {k_{\ce {SP}}}}]P}}}$.

(1)

Exchange of magnetization between the two species can then be modeled using the linear ordinary differential equation

${\displaystyle {\frac {dM_{\ce {P}}}{dt}}(t)=-R_{1{\ce {P}}}M_{P}(t)+k_{\ce {SP}}M_{S}(t)}$

where ${\displaystyle R_{1{\ce {P}}}={\frac {1}{T_{1{\ce {P}}}}}}$ denotes the rate at which the transverse magnetization decays to thermal equilibrium polarization, for the product species P.

Two-species model with bidirectional flux

The unidirectional flux model can be extended to account for bidirectional metabolic flux with forward rate ${\displaystyle k_{{\ce {SP}}}}$ and backward rate ${\displaystyle k_{PS}}$

${\displaystyle {\ce {S<=>[{{} \atop {k_{\ce {SP}}}}][{{k_{\ce {PS}}} \atop {}}]P}}}$

(2)

The differential equation describing the magnetization exchange is then

${\displaystyle {\frac {dM_{\ce {P}}}{dt}}(t)=-R_{1{\ce {P}}}M_{\ce {P}}(t)-k_{\ce {PS}}M_{\ce {P}}(t)+k_{\ce {SP}}M_{\ce {S}}(t).}$

Effect of radio-frequency excitation

Repeated radio-frequency (RF) excitation of the sample causes additional decay of the magnetization vector. For constant flip angle sequences, this effect can be approximated using a larger effective rate of decay computed as

${\displaystyle R_{1{\ce {P,eff}}}=R_{1{\ce {P}}}-{\frac {\log(\cos \alpha )}{TR}}}$

where ${\displaystyle \alpha }$ is the flip angle and ${\displaystyle TR}$ is the repetition time.^[17] Time-varying flip angle sequences can also be used, but require that the dynamics be modeled as a hybrid system with discrete jumps in the system state.^[18]

Area-under-the-curve ratio

Comparing the definite integral under the substrate and product metabolite curves has been proposed as an alternative to model-based parameter estimates as a method of quantifying metabolic activity. Under specific assumptions, the ratio

${\displaystyle {\ce {{\frac {AUC(P)}{AUC(S)}}}}}$

of area under the product curve AUC(P) to the area under the substrate curve AUC(S) is proportional to the forward metabolic rate ${\displaystyle k_{{\ce {SP}}}}$.^[19]

Rate parameter mapping

When the assumptions under which this ratio is proportional to ${\displaystyle k_{PL}}$ are not met, or there is significant noise in the collected data, it is desirable to compute estimates of model parameters directly. When noise is independent and identically distributed and Gaussian, parameters can be fit using non-linear least squares estimation. Otherwise (for example if magnitude images with Rician-distributed noise are used), parameters can be estimated by maximum likelihood estimation. The spatial distribution of metabolic rates can be visualized by estimating metabolic rates corresponding to the time series from each voxel, and plotting a heat map of the estimated rates.