Q10 (temperature coefficient)

A plot illustrating the dependence on temperature of the rates of chemical reactions and various biological processes, for several different Q₁₀ temperature coefficients. The rate ratio at a temperature increase of 10 degrees (marked by points) is equal to the Q₁₀ coefficient.

The Q₁₀ temperature coefficient is a measure of temperature sensitivity based on the chemical reactions.

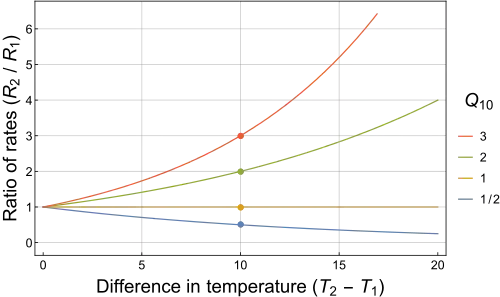
The Q₁₀ is calculated as:

${\displaystyle Q_{10}=\left({\frac {R_{2}}{R_{1}}}\right)^{10\,^{\circ }\mathrm {C} /(T_{2}-T_{1})}}$

where;

R is the rate

T is the temperature in Celsius degrees or kelvin.

Rewriting this equation, the assumption behind Q₁₀ is that the reaction rate R depends exponentially on temperature:

${\displaystyle R_{2}=R_{1}~Q_{10}^{(T_{2}-T_{1})/10\,^{\circ }\mathrm {C} }}$

Q₁₀ is a unitless quantity, as it is the factor by which a rate changes, and is a useful way to express the temperature dependence of a process.

For most biological systems, the Q₁₀ value is ~ 2 to 3.^[1]

In muscle performance

The effects of temperature on enzyme activity. Top - increasing temperature increases the rate of reaction (Q₁₀ coefficient). Middle - the fraction of folded and functional enzyme decreases above its denaturation temperature. Bottom - consequently, an enzyme's optimal rate of reaction is at an intermediate temperature.

The temperature of a muscle has a significant effect on the velocity and power of the muscle contraction, with performance generally declining with decreasing temperatures and increasing with rising temperatures. The Q₁₀ coefficient represents the degree of temperature dependence a muscle exhibits as measured by contraction rates.^[2] A Q₁₀ of 1.0 indicates thermal independence of a muscle whereas an increasing Q₁₀ value indicates increasing thermal dependence. Values less than 1.0 indicate a negative or inverse thermal dependence, i.e., a decrease in muscle performance as temperature increases.^[3]

Q₁₀ values for biological processes vary with temperature. Decreasing muscle temperature results in a substantial decline of muscle performance such that a 10 degree Celsius temperature decrease results in at least a 50% decline in muscle performance.^[4] Persons who have fallen into icy water may gradually lose the ability to swim or grasp safety lines due to this effect, although other effects such as atrial fibrillation are a more immediate cause of drowning deaths. At some minimum temperature biological systems do not function at all, but performance increases with rising temperature (Q₁₀ of 2-4) to a maximum performance level and thermal independence (Q₁₀ of 1.0-1.5). With continued increase in temperature, performance decreases rapidly (Q₁₀ of 0.2-0.8) up to a maximum temperature at which all biological function again ceases.^[5]

Within vertebrates, different skeletal muscle activity has correspondingly different thermal dependencies. The rate of muscle twitch contractions and relaxations are thermally dependent (Q₁₀ of 2.0-2.5), whereas maximum contraction, e.g., tetanic contraction, is thermally independent.^[6]

Muscles of some ectothermic species. e.g., sharks, show less thermal dependence at lower temperatures than endothermic species ^[4][7]

See also

• Arrhenius equation
• Arrhenius plot
• Isotonic (exercise physiology)
• Isometric exercise
• Skeletal striated muscle
• Tetanic contraction

References