Comment calculer une tension en physique

Coécrit par Bess Ruff, MA

En physique, la tension est la force exercée par une corde, une ficelle, un câble, etc. sur un ou plusieurs objets qui y sont fixés. Que l'objet soit juste suspendu à la verticale, qu'il oscille, qu'il se déplace sur un plan horizontal ou incliné, la corde, la ficelle, etc. subit une tension. Cette dernière est en fait une force et comme telle, elle peut mettre en mouvement l'objet en question ou même le déformer. Bien sûr, savoir calculer une tension est important pour tous ceux, élèves en particulier, qui doivent résoudre des problèmes, mais cette compétence est très souvent sollicitée dans certains métiers, comme l'ingénierie ou l'architecture. En effet, il faut être capable de savoir si une structure, sous-tendue par des câbles par exemple, va pouvoir supporter telle ou telle contrainte de poids.

Méthode 1

Méthode 1 sur 2:

Déterminer la tension dans le cas d'un seul support

1
Définissez bien les forces qui s'exercent sur les deux extrémités d'une corde. La tension d'une corde, d'un câble est la résultante de toutes les forces qui s'exercent sur ladite corde (ou câble). Nous vous rappelons que la force = masse × accélération. Partant du principe que la corde est solidement attachée, toute modification de la masse qui est suspendue au bout ou toute modification de la vitesse de ladite masse entraîne obligatoirement une modification de la tension exercée sur la corde. L'accélération due à la gravité reste constante, même si votre système est au repos : la gravité est toujours présente ! La tension qui s'exerce sur une corde s'exprime ainsi : T = (m × g) + (m × a), où « g » est l'accélération due à la gravité qui s'exerce sur l'objet fixé au bout de la corde et « a » représente toute autre accélération qui s'exercerait sur ledit objet.
- Dans le cadre d'exercices et de problèmes de physique, on suppose que la corde est idéale, en d'autres termes la corde est fine, n'a aucune masse et ne peut être ni étirée ni rompue.
- Prenons un exemple : soit un système dans lequel un poids est suspendu à une poutre via une corde (voir dessin). Ni le poids ni la corde ne bouge - le système est dit au repos. Pour qu'il reste en équilibre, il faut que la tension soit égale à la force de gravité sur le poids. Dit autrement, cela donne : Tension (F_t) = Force de gravité (F_g) = m × g.
  - Prenons l'exemple d'un poids de 10 kg, la tension sur la corde est de : 10 kg × 9,8 m/s² = 98 newtons.
2
Tenez compte de l'accélération. La gravité n'est pas la seule force qui s'exerce sur une corde, d'autres forces peuvent s'y exercer. Si, par exemple, on imprime un mouvement à l'objet suspendu, la force liée à cette accélération (masse × accélération) doit être ajoutée à la tension issue de la force de gravité.
- Si l'on reprend notre exemple du poids 10 kg suspendu à une corde laquelle n'est plus fixée sur une poutre, mais à un système qui la tire vers le haut avec une accélération de 1 m/s². Dans ce cas, on doit tenir compte de la gravité, mais aussi de cette nouvelle accélération qui est imprimée au poids, ce qui donne :
  - F_t = F_g + m × a ;
  - F_t = 98 + 10 kg × 1 m/s² ;
  - F_t = 108 newtons.
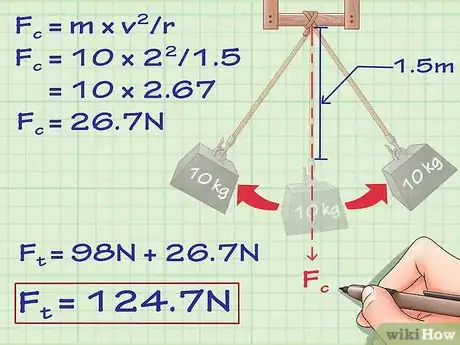
3
Tenez compte d'une éventuelle vitesse de rotation. Un objet qui se déplace selon un arc de cercle (comme un pendule) imprime une tension supplémentaire à la corde qui le soutient. C'est la force centripète. C'est une force qui s'exerce sur la corde et qui compense la force centrifuge (qui, elle, aurait tendance à faire s'éloigner l'objet de sa trajectoire). Ces deux forces sont égales dans le cas d'un objet suspendu, elles s'annulent et l'objet reste sur sa trajectoire circulaire dont le rayon est la longueur de la corde. Plus l'objet se déplace vite, plus grande est la force centripète. Cette dernière (F_c) est égale à : m × v²/r, où « m » est la masse, « v » est la vitesse et « r » est le rayon du cercle-trajectoire de l'objet en mouvement.
- Durant l'oscillation, la direction et l'intensité de la force centripète se modifient sans cesse et il en va donc de même concernant la tension sur la corde. La force centripète est parallèle à la corde et est orientée de l'objet vers le point de suspension de la corde. La force liée à la gravité agit, quant à elle, constamment du haut vers le bas. Donc, si l'on étudie le mouvement de l'objet durant son oscillation, la tension de la corde est maximale au point bas de la trajectoire (pour un pendule, on parle de « point d'équilibre »), là même où la vitesse de l'objet est maximale. Par contre, la tension de la corde est minimale au sommet de la trajectoire, là où la vitesse de l'objet est quasi nulle (l'objet ralentit, s'immobilise puis redescend)
- On reprend notre exemple, mais cette fois, l'objet n'est plus attiré vers le haut par un mouvement ascendant. Il se déplace désormais selon une trajectoire circulaire : il oscille, il se balance comme un pendule. Disons que la corde fait 1,50 m de long et qu'il a une vitesse de 2 m/s quand il est à son point le plus bas. Si vous voulez obtenir la tension de la corde quand l'objet est à son point d'équilibre (en bas avec une vitesse maximale), il faut d'abord savoir que la tension due à la gravité en cet endroit est absolument la même que lorsque l'objet était à son point d'arrêt, soit 98 newtons.Pour calculer la force centripète qui s'exerce sur la corde, on procède ainsi :
  - F_c = m × v²/r ;
  - F_c = 10 × 2²/1,5 ;
  - F_c =10 × 2,67 = 26,7 newtons ;
  - la tension totale est donc de : 98 + 26,7 = 124,7 newtons.
4
Comprenez bien que la tension due à la gravité change lorsqu'on a affaire à un objet qui oscille. Comme cela a été souligné plus haut, la direction et la magnitude de la force centripète changent quand un objet se balance. En effet, même si la force de gravité demeure inchangée et constante, la tension résultant de la gravité change également. Quand un objet oscillant n'est pas à son point d'équilibre (en bas, ici), la gravité ne s'exerce pas en totalité sur la corde, car la gravité est une force verticale et la corde forme, elle, un angle avec la verticale. Donc, la gravité n'agit qu'en partie sur la corde.
- Décomposez alors la force de gravité en 2 vecteurs pour bien visualiser la chose. Lorsqu'un objet suspendu oscille, la corde qui le soutient fait un angle « θ » avec la verticale (laquelle relie le point d'équilibre et le point d'ancrage de la corde). À n'importe quel endroit de la trajectoire du pendule, on peut décomposer la force de gravité en 2 vecteurs : la force mgsin(θ) est tangente à la trajectoire en direction du point d'équilibre et la force mgcos(θ) est parallèle à la tension de la corde, mais en sens opposé. La tension de la corde est égale à cette composante mgcos(θ), elle compense seulement une partie de la gravité à cet endroit, pas la totalité (sauf au point d'équilibre, où ces deux forces (tension et gravité) sont égales).
- Quand le pendule forme un angle de 15 degrés avec la verticale, il a une vitesse de 1,5 m/s. On trouve la tension de la façon suivante :
  - tension due à la gravité (T_g) = 98cos(15) = 98(0,96) = 94,08 newtons ;
  - force centripète (F_c) = 10 × 1,5²/1,5 = 10 × 1,5 = 15 newtons ;
  - tension totale = T_g + F_c = 94,08 + 15 = 109,08 newtons.
5
Prenez en compte les frictions. Tout objet qui est tiré par une corde sur une surface quelconque (sol, autre objet, fluide, etc.) génère une force de friction qui est transmise à la corde. Cette force de friction se calcule à l'aide de la formule suivante : Force due à la friction (qui s'écrit conventionnellement F_r) = (mu)N, avec « mu » qui est le coefficient de friction entre deux objets et N qui est la force normale qui s'exerce entre deux objets en contact, mais pas en mouvement. Cette force est différente de la friction cinétique, cette dernière n'apparaissant que lorsque l'un des deux objets se met en mouvement.
- Reprenons toujours notre objet de masse 10 kg poids. Il est désormais posé sur le sol et est tracté horizontalement au bout d'une corde. Cet objet se déplace à vitesse constante et subit à un moment donné une accélération de 1 m/s². Posons également que le coefficient de friction cinétique de ce sol soit de 0,5. La situation a connu deux changements majeurs : premièrement la corde n'endure pas totalement la gravité puisque l'objet est sur le sol ; deuxièmement, il va falloir tenir compte de la tension générée par la friction, mais aussi de celle créée par l'accélération de l'objet. Voici donc comment se présente le calcul de la tension qui s'exerce sur la corde :
  - force normale : (N) = 10 kg × 9,8 (accélération due à la gravité) = 98 newtons ;
  - force due à la friction : (F_r) = 0,5 × 98 N = 49 newtons ;
  - force due à l'accélération : (F_a) = 10 kg × 1 m/s² = 10 newtons ;
  - tension finale : F_r + F_a = 49 + 10 = 59 newtons.
Publicité

Méthode 2

Méthode 2 sur 2:

Déterminer la tension dans le cas de plusieurs supports

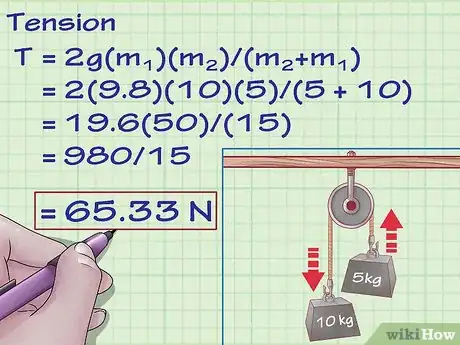
1
Étudions le cas d'une poulie qui soulève des poids avec une corde dont les deux parties sont verticales et parallèles. Les poulies sont des appareils composés d'une roue qui tourne, laquelle permet à la tension d'une corde de changer de direction. Avec une poulie simple, on a une partie de corde ou de câble qui tient un poids d'un côté (générant une tension dans la corde). Cette corde passe dans la gorge de la poulie et redescend de l'autre côté où elle est attachée à un deuxième poids. La tension est la même dans les deux cordes (si le système est immobile) et cela même si les poids sont différents. Dans le cas d'une corde passant sur une poulie et supportant deux poids de chaque côté, la tension de la corde est la suivante : 2g(m₁)(m₂)/(m₂+m₁), où « g » est l'accélération due à la gravité, « m₁ » est la masse de l'objet n° 1 et « m₂ », celle de l'objet n° 2.
- Dans les problèmes de physique, on suppose toujours qu'on a une poulie idéale, c'est-à-dire sans masse, sans friction, qui ne se casse pas, ne se déforme pas, qui ne se détache ni du plafond ni de la corde, etc.Idem pour la corde !
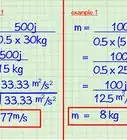
- Prenons l'exemple d'une poulie idéale qui supporte deux poids. Les deux parties de la corde sont verticales et donc parallèles. L'objet n° 1 a une masse de 10 kg, le n° 2, de 5 kg. Dans cette configuration, la tension se calcule ainsi :
  - T = 2g(m₁)(m₂)/(m₂+m₁) ;
  - T = 2(9,8)(10)(5)/(5 + 10) ;
  - T = 19,6(50)/(15) ;
  - T = 980/15 ;
  - T = 65,33 newtons.
- Vous avez noté que les deux poids étaient différents. On a supposé que les deux objets étaient fixes pour calculer notre tension de corde. Or, vous savez pertinemment que ce système ne peut pas rester en équilibre. Il va s'accélérer : le poids de 10 kg va descendre, entraînant le poids de 5 kg vers le haut.
2
Étudions le cas d'une poulie qui soulève des poids avec une corde dont les deux parties ne sont pas parallèles. Les poulies ne fonctionnent pas seulement avec une corde qui monte et descend verticalement ! Prenons l'exemple suivant : une partie de la corde est verticale et soutient un poids (c'est classique) mais l'autre bout de la corde, lui, soutient un poids qui se trouve sur un plan incliné. On a un système où la corde n'est pas parallèle, elle forme un triangle « premier poids - poulie - deuxième poids ». Dans ce cas de figure, la tension de la corde est fonction de la gravité qui s'exerce verticalement sur l'un des poids (on s'en doutait !) et est fonction de la composante de la gravité qui tend à faire glisser le deuxième poids vers le bas. Cette dernière force est parallèle au plan incliné.
- Exemple : un poids de 10 kg (m₁) pend verticalement au bout d'une corde qui passe par une poulie et à l'autre bout de cette corde, il y a un poids de 5 kg (m₂) qui est posé sur un plan incliné à 60 degrés (on part du principe qu'il n'y a pas de friction). Pour calculer la tension de la corde, il va falloir la calculer des deux côtés. Procédez comme suit :
  - Le poids qui se déplace verticalement est le plus lourd (on suppose qu'il n'y a pas de friction), il va donc descendre sous l'effet de la gravité et subir une accélération. La tension dans la corde est la force opposée à la force générée par la gravitation. Ce qu'on appelle la « force nette » (F) de cette partie de corde se calcule ainsi : F = m₁(g) - T, soit 10(9,80) - T = 98 - T.
  - Le poids qui se trouve sur le plan incliné va monter. Comme il n'y a pas de friction, le poids monte sous l'effet de la tension de la corde, mais il n'y a qu'une seule force qui l'attire vers le bas de par son poids. Comme l'objet est en pente, seule une partie de la force de gravité agit contre la tension de la corde. Cette composante est donnée par la formule : mgsin(θ). Donc, dans notre exemple, ce qu'on appelle la « force nette » (F), celle qui fait monter le poids le long du plan incliné, est égale à : F = T - m₂(g)sin(60) = T - 5(9,80)(0,87) = T - 42,63.
  - Comme la tension de la corde est uniforme quel que soit le bout, on met ces deux équations à égalité, on obtient : 98 - T = T - 42,63. On isole T d'un côté, ce qui nous donne : 2T = 140,63, soit T = 70,315 N ou T ≈ 70,32 N.
3
Étudions le cas d'un poids suspendu par plusieurs cordes. Imaginons maintenant un objet suspendu à une corde verticale, laquelle est, à son tour, accrochée à deux cordes accrochées au plafond, formant donc un angle par rapport à la verticale. La tension de la corde verticale est simple, c'est celle liée à la gravité, soit m(g). Pour les deux autres cordes, c'est un peu moins simple. Tout d'abord, si les angles d'accroche sont différents, les deux tensions seront différentes. On part du principe que les tensions dans ces deux cordes vont venir contrebalancer la tension de la corde verticale pour que le système puisse être au repos. La tension dans ces cordes transverses est fonction et du poids suspendu et de l'angle des cordes avec le plafond.
- Dans votre système en forme de Y, l'objet a une masse de 10 kg et les deux cordes du haut ont respectivement un angle de 30 et 60 degrés. Si vous cherchez à connaître la tension de chacune des cordes du haut, vous devez prendre en compte les composantes horizontales et verticales de ces deux tensions. Pour trouver T₁ (la tension de la corde à 30 degrés) et T₂ (la tension de la corde à 60 degrés), procédez comme suit :
  - Selon les lois de la trigonométrie, la relation entre T = m(g) et T₁ ou T₂ est conditionnée par le cosinus de l'angle formé par la corde en question et le plafond. Pour T₁, cos(30°) = 0,87 et pour T₂, cos(60°) = 0,5.
  - Multipliez la tension de la corde du bas (T = mg) par les cosinus de chaque angle afin de déterminer T₁ et T₂.
  - T₁ = 0,87 × m(g) = 0,887 × 10(9,8) = 85,26 newtons.
  - T₂ = 0,55 × m(g) = 0,55 × 10(9,8) = 49 newtons.
Publicité