اختلاف مركزي (رياضيات)
اللاتمركزية[1] أو التباعد المركزي في الرياضيات (Eccentricity) مصطلح يتعلق القطع الناقص (الشكل البيضوي) ، وهو مقياس لمدى ابتعاد هذا الشكل عن كونه دائريا. بالنسبة للدائرة ، فمركز الدائرة يكون دائما في وسطها ؛ أما في القطع الناقص فله مركزين منفصلين ، وهذا هو الاختلاف المركزي ، وله قيمة حسابية في الرياضيات. يصادفنا الاختلاف المركزي عند دراسة مدارات المذنبات التي تكون في شكل بيضوي.
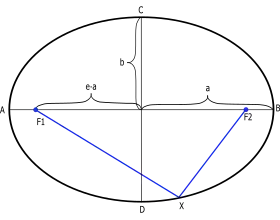
يمكن رسم القطع الناقص بفتلة f2 , x , f1 ونحرك القلم عند x حول البؤرتين فيتشكل القطع الناقص.
معظم الكواكب تدور حول الشمس تكون في مدارات في هيئة قطع الناقص وتقع الشمس في أحد بؤرتيه. من النادر جدا أن يكون مدار كوكب ما دائرة مثالية ، وانما يكون منزاحا قليلا في شكل القطع الناقص. ينطبق هذا أيضا على الأرض وهي تدور حول الشمس ؛ وكذلك ينطبق ذلك على مدار القمر في دورانه حول الأرض - يقترب أحيانا ويبتعد أحيانا أخرى (أنظر القمر الدامي).
المخروطيات
المخروطيات conic أو المقطع المخروطي conic section هي كل منحني ينتج عن قطع المخروط بمستوي في اتجاه ما.
تعريف مخروطي بالبؤرة والدليل والاختلاف المركزي
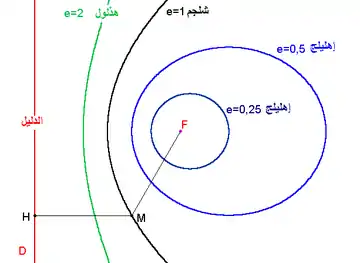

في مستوى, عندنا مستقيم D (الدليل) ونقطة F (البؤرة) و e عدد حقيقي موجب بين صفر و 1 ؛ يسمى معامل الاختلاف المركزي.
في الشكل إلى اليسار أختير معامل الاختلاف المركزي يساوي e=1
فتشكل مجموعة نقاط المستوى M التي تحقق الشرط: MF=e.MH شكل القطع الناقص.
حيث :MH المسافة بين M و D ،
ويسمى المدار الأسود قطعا ناقصا ذا البؤرة F والدليل D و«معامل الاختلاف المركزي» e=1.
في الشكل قطعين ناقصين آخرين (أزرق) أحدهما ذو اختلاف مركزي e=0,5
والآخر ذو اختلاف مركزي e=25,0 :
في حالة اختيار e=0 تنشأ دائرة.
وفي حالات e > 1 تنشأ للمدار أشكالا أخرى غير القطع الناقص .
يتشكل القطع الناقص أيضا عند قطع أسطوانة قطعا مائلا علن العمودي على محور الأسطوانة (تستطيع أن تجرب ذلك)
كذلك ينشأ القطع الناقص عندما نقطع مخروطا قطعا مائلا غير عمودي على محور المخروط .
تصنيف المخروطيات حسب قيم الاختلاف المركزي e
- إذا كان e=0، فالمخروطي يسمى: دائرة.
- إذا كان 0<e و e<1، فالمخروطي يسمى: قطع ناقص أو إهليلجا Ellipse.
- إذا كان e=1، فالمخروطي يسمى: قطعا مكافئا (شلجما) Parabola.
- إذا كان 1<e، فالمخروطي يسمى: قطعا زائدا (هذلولا) Hyperbola.
داخل وخارج مخروطي
البؤرة توجد داخل المخروطي, والدليل يوجد خارجه.
العمودي على الدليل D المار بـالبؤرة F هو محور تناظر المخروطي ويسمى المحور البؤري (أنظر أيضا الشكل 1).
رؤوس مخروطي
- إذا كانت e=1 فالمحور البؤري (fD) يقطع المخروطي في نقطة واحدة هي منتصف fD, وتسمى رأس المخروطي.
- إذا كانت e<1 فالمحور البؤري (fD) يقطع المخروطي في نقطتين مختلفتين هما رأسي المخروطي (قارن أيضا الشكل 1).
دراسة الإهليلج
خصائص إهليلج
للإهليلج محور كبير AB في الشكل 1 , ومحور صغير CD. المحوران متعامدان ويتقاطعان في نقطة تسمى مركز الإهليلج. للإهليلج (القطع الناقص) محورين تناطر ، أحدهما AB والآخر CD (شكل1).
المعادلة المختصرة للقطع الناقص
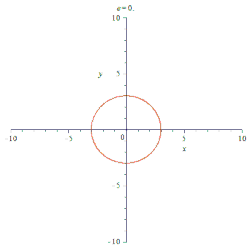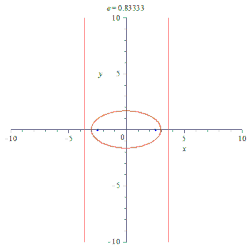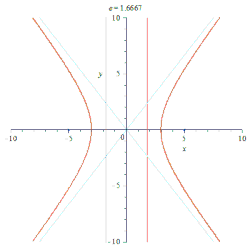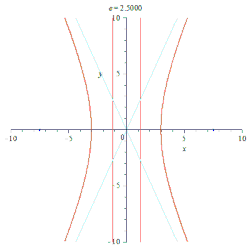
- إذا كان المحور الكبير = 2a
- و طول المحور الصغير = 2b
فإن معادلة الإهليلج يمكن كتابتها على الصورة :
حيث x , y هي أي نقطة على محيط القطع الناقص في رسم بياني عمودي المحورين.
التعريف البؤرتاني للإهليلج
الإهليلج ذو البؤرتين F و F' الذي محوره الكبير هو 2a هو مجموعة النقط M التي تحقق: MF+MF'=2a.
المعادلة البارامترية للإهليلج
انظر أيضًا
مراجع
- بنك المصطلحات السعودي نسخة محفوظة 19 يوليو 2017 على موقع واي باك مشين.
- بوابة رياضيات
- بوابة هندسة رياضية