سرعة مساحية
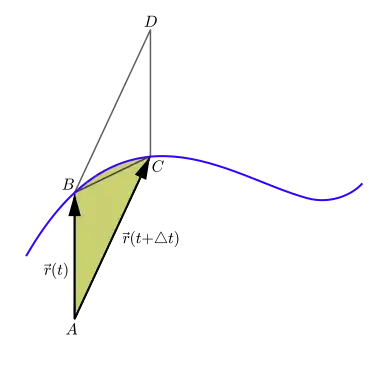
السرعة المساحية في الميكانيكا الكلاسيكية هي مقدار يعبر عن سرعة المساحة المنجرفة بواسطة متجه موضع جسم خلال حركة منحنية بالنسبة لمركز معين، كما يبين الشكل جانبه، يتحرك الجسم وفق المنحنى الأزق، في لحظة يكون الجسم في موضع وبعد مدة وجيزة، عند اللحظة يصبح الجسم في الموضع ، المساحة المنكسحة أو المساحة المنجرفة هي المساحة بالرمادي (في الشكل)، المحصورة بين القطعتين و ومنحنى الحركة، والسرعة المساحية هي مقدار هذه المساحة مقسوم على المدة الزمنية عندما تؤ، ل هذه المدة إلى الصفر.[1] ارتبط تصور السرعة المساحية بمفهوم الزخم الزاوي. ينص قانون كبلر الثاني على أن السرعة المساحية لكوكب باعتبار الشمس كمركز، تبقى ثابتة. وكان إسحاق نيوتن أول من أدرك قانون كبلر الثاني ديناميكيا وحسب قوانينه للحركة، فوجد سنة 1684 أن أي جسم يخضع لجاذبية ممركزة في مركز ثابت، يكسح سرعة مساحية ثابتة بالنسبة لزمن، ومع منتصف القرن الثامن عشر وجد مبدأ الزخم الزاوي من قبل دانييل برنولي و ليونهارت أويلر وباتريك داركي، حيث أن صياغة داركي لهذا المبدأ اعتمدت تصور المساحة المنجرفة، لهذا كان يشار إليه في أغلب الكتب القديمة باسم "مبدأ المساحات"
البعد والوحدة
بعد السرعة المساحية هو:
تعليل
الوحدة المشتقة للنظام العالمي للوحدات هي المتر المربع في الثانية.
تعابير رياضية
يعبر عن السرعة المساحية المتوسطة بـ :
تحدد السرعة المساحية اللحظية بحساب النهاية:
برهان هندسي
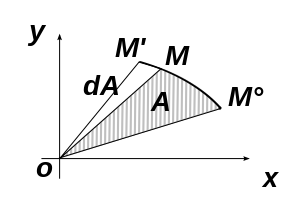
نعتبر المسار في الشكل جانبه، عند اللحظة يكون الجسم عند الموضع . وفي لحظة يصبح الجسم في الموضع . نسمي المساحة المنكسحة من اللحظة إلى اللحظة .
خلال الزمن تكسح متجهة الموضع مساحة .
إحداثيات النقطة الكارتيزية هي و . وفي النظام القطبي، هي: (الشعاع) و (الزاوية).
إحداثيات النقطة هي بالمثل و أو بالإحداثيات القطبية: و .
في الإحداثيات القطبية
لتحديد المساحة ، تُقرب إلى مساحة المثلث .
.
و منه:
نهمل الفرق الطفيف أمام قيمة ,
وكذلك تقرب إلى حيث أن الزاوية تؤول إلى الصفر.
نجد إذن مساحة المثلث المتناهي في الصغر :
- .
وبالتالي السرعة المساحية في الإحداثيات القطبية:
- .
في الإحداثيات الكارتيزية
تعطى مساحة المثلث المتناهي في الصغر بحساب المحدد:
ومنه نستخرج السرعة المساحية بالنسبة للإحداثيات الكارتيزية :
انظر أيضا
مراجع
- "معلومات عن السرعة المساحية على موقع zthiztegia.elhuyar.eus"، zthiztegia.elhuyar.eus، مؤرشف من الأصل في 11 ديسمبر 2019.