تحديد حلقي
في علوم الكمبيوتر، تحديد الحلقة أو إيجاد الحلقة عبارة عن مشكلة خوارزمية لايجاد حلقة في تسلسل لقيم مكررة.
بالنسبة لأي دالة f تقوم بربط مجموعة منتهية S بذاتها، وبأي قيمة أولية x0في S ، فإن تسلسل قيم الدوال المكررة كالتالي
يجب في النهاية استخدام نفس القيمة مرتين: يجب أن يكون هناك زوج من المؤشرات المميزة i و j بحيث يكون xi = xjيجب أن يستمر التسلسل بشكل دوري، من خلال تكرار نفس سلسة القيم من xiإلى xj − 1. تحديد الحلقة هو مشكلة إيجاد i و j، إذا كان لدينا فرضاً f و x0.
يوجد العديد من الخوارزميات المعروفة لتحديد الحلقات بسرعة وبقليل من الذاكرة. تحرك خوارزمية السلحفاة والأرنب روبرت دبليو فلويد مؤشرين بسرعات مختلفة من خلال سلسلة من القيم حتى يشير كلاهما إلى قيم متساوية. عوضاً عن ذلك، تعتمد خوارزمية برينت Brent على فكرة البحث الأسي. تستخدم كل من خوارزميات فلويد وبرنت عددًا ثابتًا من خلايا الذاكرة، وتأخذ عددًا من تقييمات الدوال التي تتناسب مع المسافة من بداية السلسلة إلى التكرار الأول. تقوم العديد من الخوارزميات بمقايضة كميات أكبر من الذاكرة من أجل تقييم أقل للدوال.
تشمل تطبيقات التحديد الحلقي اختبار جودة مولدات الأرقام العشوائية الزائفة (شبه عشوائية) و دوال هاش للتشفير، وخوارزميات نظرية العدد الحاسوبي، والكشف عن الحلقات اللانهائية في برامج الكمبيوتر والتكوينات الدورية في الأتمتة الخلوية، وتحليل الشكل الآلي لهياكل بيانات القائمة المتصلة .[1]
مثال
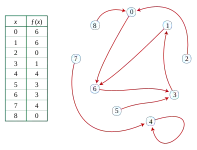
يوضح الشكل دالة f التي تربط المجموعة بذاتها. إذا بدأنا بالتعيين من x0 = 2و التطبيق بشكل متكرر f ،فسنرى سلسلة القيم كالتالي
الحلقة في سلسلة القيم هذه هي .
المراجع
- W, FloydRobert (01 أكتوبر 1967)، "Nondeterministic Algorithms"، Journal of the ACM (JACM) (باللغة الإنجليزية)، doi:10.1145/321420.321422، مؤرشف من الأصل في 23 يونيو 2020.
روابط خارجية
- غابرييل نيفاش، مشكلة اكتشاف الدورة وخوارزمية المكدس
- السلحفاة والأرنب البري ، مستودع نمط بورتلاند
- خوارزمية الكشف عن دورة فلويد (السلحفاة والأرنب البري)
- خوارزمية اكتشاف دورة برنت (السلحفاة عن بعد)
- بوابة علم الحاسوب