ترتيب انتقائي

خوارزمية الترتيب الانتقائي (بالإنجليزية: selection sort)‏ نوع من أنواع خوارزميات الترتيب وبالتحديد خوارزميات الترتيب في المكان وهذه الخوارزمية من الرتبة O n2 وهو ما يجعلها طريقة مثلى في قوائم البيانات الطويلة وعموما هي أسوأ من قرينتها من الترتيب الإدخالي.[1][2][3] الترتيب الانتقائي مشهور بسهولته وكذلك أدائه مقارنة بقرنائه الأكثر تعقيدا خصوصا عند توافر ذاكرة محدودة.

ترتيب انتقائي
بيانات عامّة
الصنف
بنية البيانات
الأداء
أسوء حالة
الحالة المُثلى
الأداء الوسطي
أسوأ حالة تعقيد مكاني
صورة متحركة توضح عملية الترتيب الانتقائي

خوارزمية

هذه الخوارزمية تعمل كما يلي:

  1. إوجد العنصر الأقل قيمة في القائمة.
  2. بدل هذا العنصر مع العنصر الأول في القائمة.
  3. كرر الخطوتين السابقاتين، ولكن هذه المرة إبدأ من العنصر التالي.

عمليا ستكون القائمة منقسمة إلى قسمين؛ الجزء الأول في القائمة سيكون مرتبا بالفعل وهو الجزء الذي يتم بناؤه أولاً بأول عن طريق إضافة العنصر الأصغر في البداية. والجزء الآخر هو الجزء محل عملية الترتيب والذي يتضاءل حجمه مع الوقت.

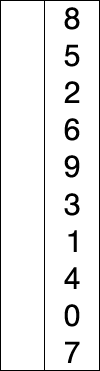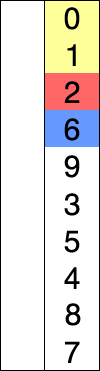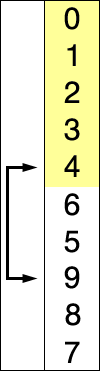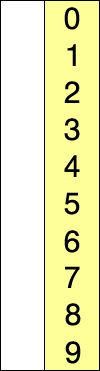
وإليكم مثال على عملية الترتيب حيث نقوم بترتيب خمسة عناصر:

64 25 12 22 11

11 25 12 22 64

11 12 25 22 64

11 12 22 25 64

11 12 22 25 64

(نلاحظ عدم وجود تغيير لإن أول رقمين هم بالفعل أصغر رقمين)

يمكن استخدام القائمة المترابطة من أجل إضافة وحذف أسرع وعلى سبيل المثال:

64 25 12 22 11

11 64 25 12 22

11 12 64 25 22

11 12 22 64 25

11 12 22 25 64

مثال بلغة C

 
/* a[0] to a[n-1] is the array to sort */
int i,j;

/* advance the position through the entire array */
/*   (could do j < n-1 because single element is also min element) */
for (j = 0; j < n-1; j++) {
    /* find the min element in the unsorted a[j .. n-1] */

    /* assume the min is the first element */
    int iMin = j;
    /* test against elements after j to find the smallest */
    for ( i = j+1; i < n; i++) {
        /* if this element is less, then it is the new minimum */
        if (a[i] < a[iMin]) {
            /* found new minimum; remember its index */
            iMin = i;
        }
    }

    if(iMin != j) {
        swap(a[j], a[iMin]);
    }
}

مراجع
  1. "معلومات عن ترتيب انتقائي على موقع rosettacode.org"، rosettacode.org، مؤرشف من الأصل في 13 فبراير 2019.
  2. "معلومات عن ترتيب انتقائي على موقع mathworld.wolfram.com"، mathworld.wolfram.com، مؤرشف من الأصل في 4 أكتوبر 2018.
  3. "معلومات عن ترتيب انتقائي على موقع xlinux.nist.gov"، xlinux.nist.gov، مؤرشف من الأصل في 30 نوفمبر 2018.
  • بوابة خوارزميات
  • بوابة علم الحاسوب
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.