ثنائية المعاوقة

مقلوب المعاوقة أو ثنائية المعاوقة هو أحد المصطلحات المستخدمة في تحليل الدوائر الكهربية، حيث أن مقلوب المعاوقة  هو . ويمكن القول أن مقلوب المعاوقة  هو المسامحة الكهربية، حيث: .

وهذا يتفق مع فكرة الازدواجية في الدوائر الكهربائية، حيث:  و [1]

ثنائيات عناصر الدوائر الكهربية
[2]
العنصر Z ثنائي العنصر Z'
المقاوم الكهربي R
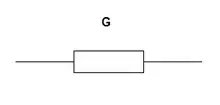الموصل الكهربي G = R
الموصل الكهربي G
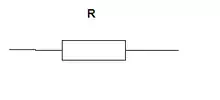المقاوم الكهربي R = G
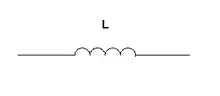الملف L
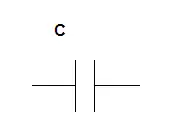المكثف C = L
المكثف C
الملف L = C
معاوقات على التوالي Z = Z1 + Z2
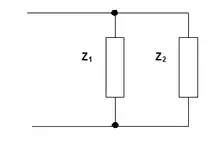معاوقات على التوازي Y = Z1 + Z2
معاوقات على التوازي 1/Z = 1/Z1 + 1/Z2
معاوقات على التوالي 1/Y = 1/Z1 + 1/Z2
مصدر جهد كهربي V
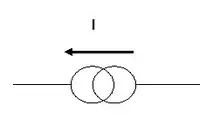مصدر تيار كهربي I = V
مصدر تيار كهربي I
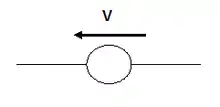مصدر جهد كهربي V = I

طريقة بيانية

هناك طريقة بيانية أسهل في الاستخدام من التعبير الرياضي:

  1. توصيل مصدر الجهد الكهربي بين كل عقدتين في الدائرة، والغرض من هذه العملية هو حفظ العقد من الضياع عند تحويل الدائرة.
  2. رسم نقطة داخل كل شبكة من الشبكات في الدائرة Z، هذه النقاط سوف تصبح عقد الدائرة Z'.
  3. يتم رسم مصدر تيار كهربي بين كل نقطة داخل الشبكة وبين مصدر الجهد الكهربي في الدائرة Z.
  4. يتم رسم ثنائية المعاوقة Z' بين العقد في الدائرة الجديدة Z'.[3]

مثال

ثنائية المعاوقة لدائرة على شكل واي من ثلاث ملفات يعطي دائرة على شكل دلتا من ثلاث مكثفات.

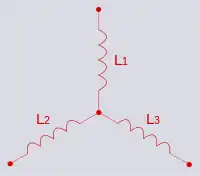دائرة على شكل حرف واي من ثلاث ملفات
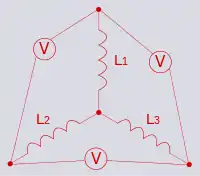توصيل مصدر الجهد الكهربي بين كل عقدتين في الدائرة
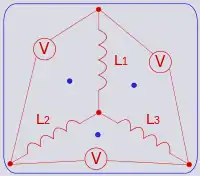رسم نقطة داخل كل شبكة
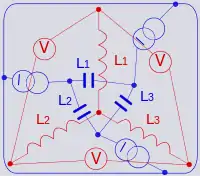يتم رسم مصدر تيار كهربي بين كل نقطة داخل الشبكة وبين مصدر الجهد الكهربي في الدائرة Z، ثم رسم ثنائية المعاوقة Z' بين العقد في الدائرة الجديدة.
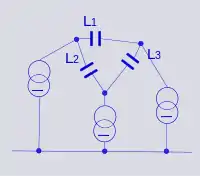دائرة ثنائية المعاوقة Z'
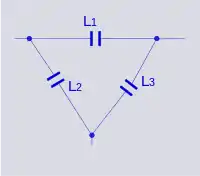حذف مصادر التيار الكهربي

انظر أيضًا

المراجع
  1. Ghosh, Smarajit, Network Theory: Analysis and Synthesis, Prentice Hall of India, pp.50-51
  2. Guillemin, Ernst A., Introductory Circuit Theory, New York: John Wiley & Sons, 1953, pp.535-539
  3. Guillemin, pp.49-52
    Suresh, pp.516-517
  • بوابة كهرباء
  • بوابة إلكترونيات
  • بوابة الفيزياء
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.